浙教版数学八年级下册5.3正方形基础检测

如图，点E在正方形ABCD对角线AC上，且EC=2.5AE，直角三角形FEG的两直角边EF，EG分别交BC，CD于M，N．若正方形边长是a，则重叠部分四边形EMCN的面积为（　　）

在平面直角坐标系中，正方形ABCD的位置如图所示，点A的坐标为（1，0），点D的坐标为（0，2）．延长CB交x轴于点A₁ ， 作正方形A₁ B₁ C₁ C；延长C₁B₁交x轴于点A₂ ， 作正方形A₂B₂C₂C₁…按这样的规律进行下去，若正方形ABCD算第一个正方形，则第2010个正方形的面积为（　　）

如图，E是边长为4的正方形ABCD的对角线BD上一点，且BE=BC，P为CE上任意一点，PQ⊥BC于点Q，PR⊥BR于点R，则PQ+PR的值是（　　）

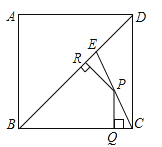如图，在正方形ABCD中，AB=4，P是线段AD上的动点，PE⊥AC于点E，PF⊥BD于点F，则PE+PF的值为（　　）

如图，在正方形ABCD的外侧，作等边三角形ADE，连接CE，与对角线BD交于F，则∠BFC为（　　）

如图，在平面直角坐标系中，四边形ABCO是正方形，已知点C的坐标为（$\sqrt{3}$ ， 1），则点B的坐标为（　　）

如图，已知在正方形ABCD中，点E、F分别在BC、CD上，△AEF是等边三角形，连接AC交EF于G，给出下列结论：

①BE=DF；②∠DAF=15°；③AC垂直平分EF；④BE+DF=EF．

其中结论正确的共有（　　）

如图：A，D，E在同一条直线上，AD=3，DE=1，BD，DF分别为正方形ABCD，正方形DEFG的对角线，则三角形△BDF的面积为（　　）

如图，在正方形ABCD的外侧，作等边三角形ADE，则∠AEB=（　　）

如图，正方形的边长为4cm，则图中阴影部分的面积为（　　）cm² ．

如图，在平面直角坐标系中，点A（$\sqrt{3}$ ， 0），点B（0，1），作第一个正方形OA₁C₁B₁且点A₁在OA上，点B₁在OB上，点C₁在AB上；作第二个正方形A₁A₂C₂B₂且点A₂在A₁A上，点B₂在A₁C₂上，点C₂在AB上…，如此下去，则点C_n的纵坐标为 ．

如图，正方形ABCD的边长为4+2$\sqrt{2}$ ， 点E在对角线BD上，且∠BAE=22.5°，EF⊥AB，垂足为点F，则EF的长是 ．

如图，边长分别为3和5的两个正方形ABCD和CEFG并排放在一起，连结BD并延长交EG于点T，交FG于点P，则ET的长为 

正方形A₁B₁C₁O、A₂B₂C₂C₁、A₃B₃C₃C₂、…，按如图所示的方式放置．点A₁、A₂、A₃、…和点C₁、C₂、C₃、…分别在直线y=x+1和x轴上，则第2015个正方形A₂₀₁₅B₂₀₁₅C₂₀₁₅C₂₀₁₄的边长为 ．

已知正方形ABCD的边长为a，两条对角线AC、BD相交于点O，P是射线AB上任意一点，过P点分别作直线AC、BD的垂线PE、PF，垂足为E、F．

（1）如图1，当P点在线段AB上时，PE+PF的值是否为定值？如果是，请求出它的值；如果不是，请加以说明．

（2）如图2，当P点在线段AB的延长线上时，求PE﹣PF的值．

（1）如图1，4条直线l₁、l₂、l₃、l₄是一组平行线，相邻2条平行线的距离都是2cm，正方形ABCD的4个顶点A、B、C、D分别在l₁、l₃、l₄、l₂上，求该正方形的面积；

（2）如图2，把一张矩形卡片ABCD放在每格宽度为18mm的横格纸中，恰好四个顶点都在横格线上，已知∠1=36°，求长方形卡片的周长．（精确到1mm）（参考数据：sin36°≈0.60，cos36°≈0.80，tan36°≈0.75）

已知正方形ABCD和等腰Rt△BEF，BE=EF，∠BEF=90°，按图放置，使点E在BC上，取DF的中点G，连结EG、CG．

（1）请添加一条辅助线，构造一个和△FEG全等的三角形，并证明它们全等．

（2）探索EG、CG的数量关系和位置关系，并证明．

如图，在正方形ABCD中，点E在对角线AC上，点F在边BC上，联结BE、DF，DF交对角线AC于点G，且DE=DG；

（1）求证：AE=CG；

（2）求证：BE∥DF．

如图，P为正方形ABCD对角线AC上一动点，EF⊥AC且交AD于E，交CD的延长线于点G，连接CE和AG．

（1）求证：△ADG≌△CDE；

（2）当CE平分∠ACD时，求tan∠AGD．

如图，在正方形ABCD中，点E在对角线AC上，点F在边BC上，联结BE、DF，DF交对角线于点P，且DE=DP．

（1）求证：AE=CP；

（2）求证：BE∥DF．

（1）如图1，直线a∥b∥c∥d，且a与b，c与d之间的距离均为1，b与c之间的距离为2，现将正方形ABCD如图放置，使其四个顶点分别在四条直线上，求正方形的边长；

（2）在（1）的条件下，探究：将正方形ABCD改为菱形ABCD，如图2，当∠DCB=120°时，求菱形的边长．

如图，在正方形ABCD中，点E在对角线AC上，点F在边BC上，连接BE、DF，DF交对角线AC于点G，且DE=DG．

（1）求证：AE=CG；

（2）试判断BE和DF的位置关系，并说明理由．