浙教版数学八年级下册5.1矩形基础检测

试卷更新日期：2016-04-16 类型：同步测试

进入出卷网下载

一、单选题

1. 下列说法中的错误的是（　　）

A、一组邻边相等的矩形是正方形 B、一组邻边相等的平行四边形是菱形 C、一组对边相等且有一个角是直角的四边形是矩形 D、一组对边平行且相等的四边形是平行四边形

查看试题解析
2.
如图，在矩形ABCD中，E，F分别是边AB，CD上的点，AE=CF，连接EF，BF，EF与对角线AC交于点O，且BE=BF，∠BEF=2∠BAC，FC=2，则AB的长为（　　）

A、 $8 \sqrt{3}$ B、8 C、 $4 \sqrt{3}$ D、6

查看试题解析
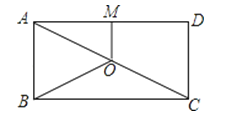
3.
如图，O是矩形ABCD的对角线AC的中点，M是AD的中点，若AB=5，AD=12，则四边形ABOM的周长为（　　）

A、17 B、18 C、19 D、20

查看试题解析
4.
一个矩形被分成不同的4个三角形，其中绿色三角形的面积占矩形面积的15%，黄色的三角形的面积是21cm² ，则该矩形的面积为（　　）

A、60cm² B、70cm² C、120cm² D、140cm²

查看试题解析
5.
如图，在矩形ABCD中，对角线AC、BD相交于点O，若∠ACB=30°，AB=2，则BD的长为（　　）

A、4 B、3 C、2 D、1

查看试题解析
6.
如图，矩形的两条对角线的一个交角为60°，两条对角线的长度的和为20cm，则这个矩形的一条较短边的长度为（　　）

A、10cm B、8cm C、6cm D、5cm

查看试题解析
7.
如图，矩形ABCD中，AB=8，AD=6，将矩形ABCD绕点B按顺时针方向旋转后得到矩形A′BC′D′．若边A′B交线段CD于H，且BH=DH，则DH的值是（　　）

A、 $\frac{7}{4}$ B、 $8 - 2 \sqrt{3}$ C、 $\frac{25}{4}$ D、 $6 \sqrt{2}$

查看试题解析
8.
如图，在矩形ABCD中，O为AC中点，EF过O点且EF⊥AC分别交DC于F，交AB于E，点G是AE中点且∠AOG=30°，则下列结论正确的个数为（　　）
（1）DC=3OG；（2）OG= $\frac{1}{2}$ BC；（3）△OGE是等边三角形；（4）S_△AOE= $\frac{1}{6}$ S_ABCD ．

A、1个 B、2个 C、3个 D、4个

查看试题解析
9.
在如图所示的矩形ABCD中，已知MN丄MC，且M为AD的中点，AN=2，tan∠MCN= $\frac{1}{4}$ ，则AB等于（　　）

A、32 B、28 C、36 D、40

查看试题解析
10. 在△ABC中，CO为AB边上的中线，且OC= $\frac{1}{2}$ AB，以点O为圆心，OC长为半径画圆，延长CO交⊙O于点D，连结AD，BD，则四边形ADBC是（　　）

A、正方形 B、矩形 C、菱形 D、邻边相等的四边形

查看试题解析
11. 下列说法正确的是（　　）

A、对角线互相垂直且相等的四边形是菱形 B、对角线相等的四边形是矩形 C、对角线互相垂直的四边形是平行四边形 D、对角线相等且互相平分的四边形是矩形

查看试题解析
12. 在四边形ABCD中，AB∥DC，AD∥BC，如果添加一个条件，即可推出该四边形是矩形，那么这个条件可以是（　　）

A、∠D=90° B、OH=4 C、AD=BC D、Rt△AHB

查看试题解析
13.
如图，要使平行四边形ABCD变为矩形，需要添加的条件是（　　）

A、AC=BD B、AD=BC C、AB=CD D、AB=BC

查看试题解析
14. 已知四边形ABCD是平行四边形，对角线AC与BD相交于点O，下列结论中不正确的是（　　）

A、当AB=BC时，四边形ABCD是菱形 B、当AC⊥BD时，四边形ABCD是菱形 C、当OA=OB时，四边形ABCD是矩形 D、当∠ABD=∠CBD时，四边形ABCD是矩形

查看试题解析
15. 在数学活动课上，老师和同学们判断一个四边形门框是否为矩形，下面是一个学习小组拟定的方案，其中正确的是（　　）

A、测量对角线是否相互平分 B、测量两组对边是否分别相等 C、测量对角线是否相等 D、测量其中三个角是否都为直角

查看试题解析

二、填空题

16.
如图，平行四边形ABCD的对角线相交于点O，请你添加一个条件．（只添一个即可），使平行四边形ABCD是矩形．

查看试题解析
17.
如图，矩形ABCD中，DE⊥AC于点E，∠EDC：∠EDA=1：3，且AC=12，则DE的长度是　（结果用根号表示）．

查看试题解析
18.
如图，矩形OABC在第一象限，OA，OC分别于x轴，y轴重合，面积为6．矩形与双曲线y= $\frac{k}{x}$ （x＞0）交BC于M，交BA于N，连接OB，MN，若2OB=3MN，则k=

查看试题解析
19.
如图，矩形ABCD中，AB=2AD，AP平分∠DAB，且AP⊥DP于点P，连接CP，则sin∠DCP的值是　　．

查看试题解析
20.
如图，在长方形ABCD中，AB：BC=3：5，以点B为圆心，BC的长为半径画弧，交边AD于点E．若AE•DE=16，则长方形ABCD的面积为．

查看试题解析

三、解答题

21.
如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC．设MN交∠ACB的平分线于点E，交∠ACB的外角平分线于点F．
（1）求证：OE=OF；
（2）若CE=8，CF=6，求OC的长；
（3）当点O在边AC上运动到什么位置时，四边形AECF是矩形？并说明理由．

查看试题解析
22.
如图，在▱ABCD中，∠ABD的平分线BE交AD于点E，∠CDB的平分线DF交BC于点F，连接BD．
（1）求证：△ABE≌△CDF；
（2）若AB=DB，求证：四边形DFBE是矩形．

查看试题解析
23.
如图，矩形ABCD的边AD是菱形AEDF的一条对角线，且点E在矩形ABCD的边BC上．
（1）求证：△ABE≌△DCE；
（2）直接写出当矩形边长AD与AB之间满足什么关系时，菱形AEDF为正方形．

查看试题解析
24.
如图：在矩形ABCD中，AD=60cm，CD=120cm，E、F为AB边的三等分点，以EF为边在矩形内作等边三角形MEF，N为AB边上一点，EN=10cm；
请在矩形内找一点P，使△PMN为等边三角形（画出图形，并直接写出△PMF的面积）．

查看试题解析
25.
如图，四边形ABCD是矩形，点E是边AD的中点．
求证：EB=EC．

查看试题解析