浙教版数学八年级下册4.5三角形的中位线基础练习
试卷更新日期：2016-04-16 类型：同步测试
一、单选题
-
1.
如图，A，B两地被池塘隔开，小明通过下列方法测出了A，B间的距离：先在AB外选一点C，然后测出AC，BC的中点M，N，并测量出MN的长为12m，由此他就知道了A，B间的距离，有关他这次探究活动的描述错误的是（ ）
A、MN∥AB B、AB=24m C、△CMN∽△CAB D、△CMN与四边形ABMN的面积之比为1：22.如图，在四边形ABCD中，P是对角线BD的中点，E、F分别是AB、CD的中点，AD=BC，∠PEF=30°，则∠EPF的度数是（ ）
A、120° B、150° C、135° D、140°3.如图，已知△ABC的周长是1，连接△ABC三边的中点构成第二个三角形，再连接第二个三角形三边的中点构成第三个三角形…依此类推，则第2015个三角形的周长为（ ）
A、 B、 C、 D、4. 在△ABC中，D、E分别为AB、AC边上中点，且DE=6，则BC的长度是（ ）A、3 B、6 C、9 D、125.如图，D、E、F分别为Rt△ABC中AB、AC、BC的中点，AB=2 ， 则DC和EF的大小关系是（ ）
A、DC＞EF B、DC＜EF C、DC=EF D、无法比较6.如图，AD，AE分别是△ABC的角平分线和中线，CG⊥AD于F，交AB于G，若AB=8，AC=6，则EF的长为（ ）
A、2 B、 C、1 D、7.如图，在△ABC中，D、E分别是边AB、AC的中点，若BC=6，则DE的长为（ ）
A、2 B、3 C、4 D、68.如图，D、E分别是△ABC两边的中点，△ADE的面积记为S1 ， 四边形DBCE的面积记为S2 ， 则下列结论正确的是（ ）
A、S1=S2 B、S2=2S1 C、S2=3S1 D、S2=4S19. 如图，在△ABC中，AB=5，BC=6，AC=7，点D，E，F分别是△ABC三边的中点，则△DEF的周长为（ ）
A、9 B、10 C、11 D、1210.如图，D、E分别是△ABC的边AB、AC上的点，且AD=DB，AE=EC，若DE=4，则BC长为（ ）
A、2 B、4 C、6 D、811.如图，A，B两点被池塘隔开，在AB外选一点C，连接AC和BC，通过测量分别取AC，BC的中点D和E，量得DE长210米，则A，B两点间的距离为（ ）
A、280米 B、300米 C、420米 D、无法确定12.如图所示，▱ABCD中，对角线AC，BD交于点O，E是CD中点，连接OE，若OE=3cm，则AD的长为（ ）
A、3cm B、6cm C、9cm D、12cm13.如图，点D、E、F分别是△ABC中AB、BC、AC边上的中点，点M、N、P分别是DE、EF、DF的中点．若△ABC的周长为24，则△PMN的周长为（ ）
A、6 B、8 C、10 D、1214.如图，△ABC的中线BE与CD交于点G，连接DE，下列结论不正确的是（ ）
A、点G是△ABC的重心 B、DE∥BC C、△ABC的面积=2△ADE的面积 D、BG=2GE15. 已知三角形的3条中位线分别为3cm、4cm、6cm，则这个三角形的周长是（ ）A、3cm B、26cm C、24cm D、65cm二、填空题
-
16.
如图，点D、E、F分别是△ABC三边的中点，且AB=AC，则图中的四边形 是菱形．
17.如图，∠ACB=90°，D为AB的中点，连接DC并延长到E，使CE=CD，过点B作BF∥DE，与AE的延长线交于点F．若AB=6，则BF的长为
18.如图，△ABC中，AB=AC，以AC为斜边作Rt△ADC，使∠ADC=90°，∠CAD=∠CAB=26°，E、F分别是BC、AC的中点，则∠EDF等于
19.如图，在Rt△ABC中，∠C=90°，CD是AB边上的中线，且CD=5，则△ABC的中位线EF的长是
三、解答题
-
20.
如图，在△ABC中，若∠B=2∠C，AD⊥BC，E为BC边中点，求证：AB=2DE．
21.如图，在锐角三角形ABC中，AD⊥BC于D，E、F、G分别是AC、AB、BC的中点．求证：FG=DE．
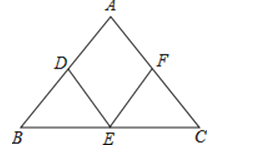
22.如图，点D、E、F分别是△ABC各边中点．求证：四边形ADEF是平行四边形．
23.如图，已知在△ABC中，DE∥BC交AC于点E，交AB于点D，DE=BC
求证：D、E分别是AB、AC的中点．
24.如图，已知∠1+∠2=180°，∠3=∠B．
（1）试判断∠AED与∠ACB的大小关系，并说明你的理由．
（2）若D、E、F分别是AB、AC、CD边上的中点，S四边形ADFE=4（平方单位），求S△ABC ．
