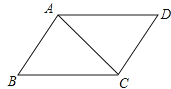
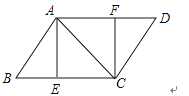
浙教版数学八年级下册4.2平行四边形基础练习

试卷更新日期：2016-04-16 类型：同步测试

进入出卷网下载

一、单选题

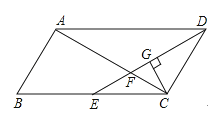
1.
如图，▱ABCD中，AB=3cm，AD=6cm，∠ADC的角平分线DE交BC于点E，交AC于点F，CG⊥DE，垂足为G，DG= $\frac{3}{2} \sqrt{3}$ cm，则EF的长为（　　）

A、2cm B、 $\sqrt{3}$ cm C、1cm D、 $\frac{2}{3} \sqrt{3}$ cm

查看试题解析
2.
如图，在平行四边形ABCD中，对角线AC、BD相交于点O．如果BD=12，AC=10，BC=m，那么m的取值范围是（　　）

A、10＜m＜12 B、2＜m＜22 C、1＜m＜11 D、5＜m＜6

查看试题解析
3.
在▱ABCD中，AC⊥AD，∠B=30°，AC=2，则▱ABCD的周长是（　　）

A、4+2 $\sqrt{3}$ B、8 C、8+4 $\sqrt{3}$ D、16

查看试题解析
4.
如图，在平行四边形ABCD中，AE⊥BC于E，AF⊥CD于F，∠EAF=45°，且AE+AF=2 $\sqrt{2}$ ，则平行四边形ABCD的周长是（　　）

A、2 B、4 $\sqrt{2}$ C、4 D、8

查看试题解析
5.
如图，在平行四边形ABCD中，过对角线AC与BD的交点O作AC的垂线交AD于点E，连接CE．若AB=4，BC=6，则△CDE的周长是（　　）

A、7 B、10 C、11 D、12

查看试题解析
6.
如图，平行四边形ABCD中，E，F分别为AD，BC边上的一点，增加下列条件，不能得出BE∥DF的是（　　）

A、AE=CF B、BE=DF C、∠EBF=∠FDE D、∠BED=∠BFD

查看试题解析
7. 已知平行四边形ABCD的对角钱AC与BD相交于点O，AB⊥AC，若AB=2，AC=8，则对角线BD的长是（　　）

A、2 $\sqrt{2}$ B、2 $\sqrt{5}$ C、4 $\sqrt{2}$ D、4 $\sqrt{5}$

查看试题解析
8.
如图，在平行四边形ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，则下列结论中一定成立的是（　　）
①∠DCF= $\frac{1}{2}$ ∠BCD；②EF=CF；③S_△_BEC=2S_△_CEF；④∠DFE=3∠AEF．

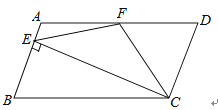A、①② B、②③④ C、①②④ D、①②③④

查看试题解析
9.
在平行四边形ABCD中，AC与BD相交于0，AE⊥BD于E，CF⊥BD于F，则图中的全等三角形共（　　）

A、5对 B、6对 C、7对 D、8对

查看试题解析
10. 如图，在▱ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，则下列结论：（1）∠DCF= $\frac{1}{2}$ ∠BCD，（2）EF=CF；（3）S_△_BEC=2S_△_CEF；（4）∠DFE=3∠AEF，其中正确结论的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
11.
如图，在平行四边形ABCD中，AD=7，CE平分∠BCD交AD边于点E，且AE=4，则AB的长为（　　）

A、4 B、3 C、 $\frac{5}{2}$ D、2

查看试题解析
12.
如图，以平行四边形ABCD的边CD为斜边向内作等腰直角△CDE，使AD=DE=CE，∠DEC=90°，且点E在平行四边形内部，连接AE、BE，则∠AEB的度数是（　　）

A、120° B、135° C、150° D、45°

查看试题解析
13. 在面积为60的▱ABCD中，过点A作AE⊥直线BC于点E，作AF⊥直线CD于点F，若AB=10，BC=12，则CE+CF的值为（　　）

A、22+11 $\sqrt{3}$ B、22﹣11 $\sqrt{3}$ C、22+11 $\sqrt{3}$ 或22﹣11 $\sqrt{3}$ D、22+11 $\sqrt{3}$ 或2+ $\sqrt{3}$

查看试题解析
14.
如图，在▱ABCD中，∠A=70°，将▱ABCD折叠，使点D、C分别落在点F、E处（点F、E都在AB所在的直线上），折痕为MN，则∠AMF等于（　　）

A、70° B、40° C、30° D、20°

查看试题解析
15.
如图，▱ABCD中，AB=4，BC=6，AC的垂直平分线交AD于点E，则△CDE的周长是（　　）

A、6 B、8 C、10 D、12

查看试题解析

二、填空题

16.
如图，在平面直角坐标系中，四边形OABC是平行四边形，O（0，0），A（1，﹣2），B（3，1），则C点坐标为 .

查看试题解析
17.
如图，▱ABCD中，E为AD边上一点，AE=AB，AF⊥AB，交线段BE于点F，G为AE上一点，AG：GE=1：5，连结GF并延长交边BC于点H．若GE：BH=1：2，则tan∠GHB= .

查看试题解析
18.
如图，在▱ABCD中，∠B=80°，∠ADC的角平分线DE与BC交于点E．若BE=CE，则∠DAE=度．

查看试题解析
19.
如图，在▱ABCD中，DB=DC，∠C=70°，AE⊥BD于E，则∠DAE=　

查看试题解析
20.
如图，在▱ABCD中，AD=4，AB=8，∠A=30°，以点A为圆心，AD的长为半径画弧交AB于点E，连接CE，则阴影部分的面积是　．（结果保留π）

查看试题解析

三、解答题

21.
已知：如图，▱ABCD中，∠BCD的平分线交AB于点E，交侧的延长线于点F．
求证：AE=AF．

查看试题解析
22.
已知平行四边形ABCD的对角线交于点O，点P是直线BD上任意一点（异于B、O、D三点），过P点作平行于AC的直线交直线AD于点E，交直线BA于点F，当点P在线段BD上时，易证得：AC=PE+PF（如图①所示）．当点P在线段BD的延长线上（如图②所示）和当点P在线段DB的延长线上（如图③所示）两种情况时，探究线段AC、PE、PF之间的数量关系，并对图③的结论进行证明．

查看试题解析
23.
如图，在▱ABCD中，点O是AC与BD的交点，过点O的直线EF与AB、CD的延长线分别交于点E、F．

(1)、求证：△BOE≌△DOF

(2)、当EF⊥AC时，四边形AECF是怎样的特殊四边形？证明你的结论

查看试题解析
24.
如图，在▱ABCD中，E为BC边上的一点，将△ABE沿AE翻折得到△AFE，点F恰好落在线段DE上．

(1)、求证：∠FAD=∠CDE

(2)、当AB=5，AD=6，且tan∠ABC=2时，求线段EC的长．

查看试题解析
25.
已知ABCD是平行四边形，用尺规分别作出△BAC与△DAC共公边AC上的高BE、DF．求证：BE=DF．

查看试题解析
26.
如图，已知▱ABCD中，AE平分∠BAD，CF平分∠BCD，分别交CD，AB于E，F．

(1)、作∠BCD的角平分线CF（尺规作图，保留痕迹，不写作法）

(2)、求证：AE=CF

查看试题解析
27.
如图，平行四边形ABCD中，AE⊥BC，CF⊥AD，垂足分别是E、F．求证：△ABE≌△CDF．

查看试题解析

四、综合题

28.
已知，如图，在▱ABCD中，点E在边AB上，连接CE．

(1)、尺规作图（保留作图痕迹，不必写出作法）；以点A为顶点，AB为一边作∠FAB=∠CEB，AF交CD于点F

(2)、求证：AF=CE

查看试题解析