初中数学人教版八年级下学期 第十九章 19.2.3 一次函数与方程、不等式
试卷更新日期:2020-03-24 类型:同步测试
一、单选题
-
1. 函数 的图像与函数 =- +3的图像平行,且与y轴的交点为M(0,2),则函数表达式为( )A、 = +3 B、 = +2 C、 =- +3 D、 =- +22. 如图,已知一次函数 的图象为直线,则关于x的方程 的解为 ( )
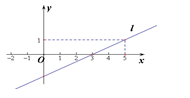 A、 B、 C、 D、3. 一次函数y=﹣2x+3的图象和y=kx﹣b的图象相交于点A(m,1),则关于x,y的二元一次方程 的解为( )A、 B、 C、 D、4. 直线y=2x﹣6与x轴的交点坐标是( )A、(0,3) B、(3,0) C、(0,﹣6) D、(﹣3,0)5. 如图,一次函数y=2x+1的图象与坐标轴分别交于A,B两点,O为坐标原点,则△AOB的面积为( )
A、 B、 C、 D、3. 一次函数y=﹣2x+3的图象和y=kx﹣b的图象相交于点A(m,1),则关于x,y的二元一次方程 的解为( )A、 B、 C、 D、4. 直线y=2x﹣6与x轴的交点坐标是( )A、(0,3) B、(3,0) C、(0,﹣6) D、(﹣3,0)5. 如图,一次函数y=2x+1的图象与坐标轴分别交于A,B两点,O为坐标原点,则△AOB的面积为( )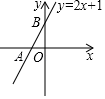 A、 B、 C、2 D、4
A、 B、 C、2 D、4二、填空题
-
6. 如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x,y的二元一次方程组 的解是 .
 7. 已知一次函数 的图象与两坐标轴围成的三角形的面积为12,则 的值为.8. 一次函数 的图象与x轴的交点坐标是 ,与y轴的交点坐标是.9. 如图,直线y=kx+b(k>0)与x轴的交点为(﹣2,0),则关于x的不等式kx+b<0的解集是 .
7. 已知一次函数 的图象与两坐标轴围成的三角形的面积为12,则 的值为.8. 一次函数 的图象与x轴的交点坐标是 ,与y轴的交点坐标是.9. 如图,直线y=kx+b(k>0)与x轴的交点为(﹣2,0),则关于x的不等式kx+b<0的解集是 .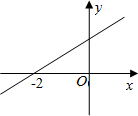
三、综合题
-
10. 如图,直线y=x+3分别与x轴、y轴交于点A、C , 直线y=mx+ 分别与x轴、y轴交于点B、D , 直线AC与直线BD相交于点M(﹣1,b)
 (1)、不等式x+3≤mx+ 的解集为 .(2)、求直线AC、直线BD与x轴所围成的三角形的面积.11. 张庄甲、乙两家草莓采摘园的草莓销售价格相同,“春节期间”,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为x(千克),在甲园所需总费用为y甲(元),在乙园所需总费用为y乙(元),y甲、y乙与x之间的函数关系如图所示,折线OAB表示y乙与x之间的函数关系.
(1)、不等式x+3≤mx+ 的解集为 .(2)、求直线AC、直线BD与x轴所围成的三角形的面积.11. 张庄甲、乙两家草莓采摘园的草莓销售价格相同,“春节期间”,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为x(千克),在甲园所需总费用为y甲(元),在乙园所需总费用为y乙(元),y甲、y乙与x之间的函数关系如图所示,折线OAB表示y乙与x之间的函数关系. (1)、甲采摘园的门票是元,两个采摘园优惠前的草莓单价是每千克元;(2)、当x>10时,求y乙与x之间的函数关系式;(3)、游客在“春节期间”采摘多少千克草莓时,甲、乙两家采摘园的总费用相同.12. 某农机租赁公司共有50台收割机,其中甲型20台、乙型30台,现将这50台联合收割机派往A,B两地区收割小麦,其中30台派往A地区,20台派往B地区,两地区与该农机公司商定的每天租赁价格如下表:
(1)、甲采摘园的门票是元,两个采摘园优惠前的草莓单价是每千克元;(2)、当x>10时,求y乙与x之间的函数关系式;(3)、游客在“春节期间”采摘多少千克草莓时,甲、乙两家采摘园的总费用相同.12. 某农机租赁公司共有50台收割机,其中甲型20台、乙型30台,现将这50台联合收割机派往A,B两地区收割小麦,其中30台派往A地区,20台派往B地区,两地区与该农机公司商定的每天租赁价格如下表:每台甲型收割机的租金
每台乙型收割机的租金
A地区
1800元
1600元
B地区
1600元
1200元
(1)、设派往A地区x台乙型联合收割机,租赁公司这50台联合收割机天获得的租金为y元,求y关于x的函数关系式,并写出自变量的取值范围:(2)、若使农机租赁公司这50台收割机一天所获租金不低于79600元,为农机租赁公司拟出一个分派方案,使该公司50台收割机每天获得租金最高,并说明理由.