四川省自贡市富顺三中、代寺学区2018-2019学年八年级下学期数学期中考试试卷

试卷更新日期：2020-03-24 类型：期中考试

进入出卷网下载

一、单选题

1. 下列式子中，属于最简二次根式的是

A、 $\sqrt{9}$ B、 $\sqrt{7}$ C、 $\sqrt{20}$ D、 $\sqrt{\frac{1}{3}}$

查看试题解析
2. 下列四组数为一个三角形的边长，可以组成直角三角形的是（）

A、5,8,7 B、2,3,4 C、24,7,25 D、5,5,6

查看试题解析
3. 已知 $m = (- \frac{\sqrt{3}}{3}) \times (- 2 \sqrt{21})$ ，则有（）

A、 $5 < m < 6$ B、 $4 < m < 5$ C、 $- 5 < m < - 4$ D、 $- 6 < m < - 5$

查看试题解析
4. 如图，一圆柱高为8cm，底面周长为30cm，蚂蚁在圆柱表面爬行，从点A爬到点B的最短路程是（）

A、15cm B、17cm C、18cm D、30cm

查看试题解析
5. 若 $\sqrt{12}$ ＋ $\sqrt{y}$ ＝ $\sqrt{27}$ ，则y的值为（）

A、8 B、15 C、3 D、2

查看试题解析
6. 如图，在▱ABCD中，对角线AC与BD相交于点O，E是边CD的中点，连结 $OE .$ 若 $∠ ABC = 60^{\circ}$ ， $∠ BAC = 80^{\circ}$ ，则 $∠ 1$ 的度数为（）

A、 $50^{\circ}$ B、 $40^{\circ}$ C、 $30^{\circ}$ D、 $20^{\circ}$

查看试题解析
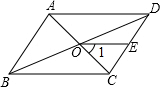7. 四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（）

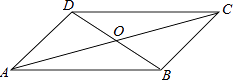A、AB∥DC，AD∥BC B、AB=DC，AD=BC C、AO=CO，BO=DO D、AB∥DC，AD=BC

查看试题解析
8. 如图，在四边形ABCD中，∠ABC=90°，∠BAD=60°，AC=AD，AC平分∠BAD，M，N分别为AC，CD的中点，BM的延长线交AD于点E，连接MN，BN．对于下列四个结论：①MN∥AD；②BM=MN；③△BAE≌△ACB；④AD= $\sqrt{2}$ BN，其中符合题意结论的序号是（）

A、①②③④ B、①②③ C、①②④ D、①②

查看试题解析

二、填空题

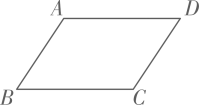
9. 如图，在四边形ABCD中，已知AB=CD，再添加一个条件（写出一个即可，图形中不再添加助线），则四边形ABCD是平行四边形．

查看试题解析
10. 函数y= $\sqrt{x - 2}$ 中，自变量x的取值范围是；实数2﹣ $\sqrt{3}$ 的倒数是．

查看试题解析
11. 函数 $y = (k + 1) x + k^{2} - 1$ 中，当 $k$ 满足时，它是一次函数.

查看试题解析
12. 若正多边形的一个内角等于140°，则这个正多边形的边数是．

查看试题解析
13. 如图，将一个正三角形纸片剪成四个全等的小正三角形，再将其中的一个按同样的方法剪成四个更小的正三角形，……如此继续下去，结果如下表：则a_n＝（用含n的代数式表示）．

所剪次数

1

2

3

4

…

n

正三角形个数

4

7

10

13

…

a_n

查看试题解析

三、解答题

14. 如图，在△ABC中，CE，BF是两条高，若∠A＝70°，∠BCE＝30°，求∠EBF与∠FBC的度数．

查看试题解析
15. 已知y＋6与x成正比例，且当x＝3时，y＝－12，求y与x的函数关系式．

查看试题解析
16. 如图，在△ABC中，DM，EN分别垂直平分AC和BC，交AB于M，N两点，DM与EN相交于点F．

(1)、若△CMN的周长为15cm，求AB的长；

(2)、若∠MFN＝70°，求∠MCN的度数．

查看试题解析
17. 已知 $x = \frac{1}{2}$ ,求 $\frac{x^{2} - 1}{x^{2} - 2 x + 1} + \frac{x^{2} - 2 x}{x - 2}$ 的值

查看试题解析
18. 作图：

(1)、在图1中，画出△CDE关于直线AB的对称图形 $△ C^{'} D^{'} E^{'}$

(2)、在图2中，已知∠AOB和C、D两点，在∠AOB内部找一点P，使PC=PD，且P到∠AOB的两边OA、OB的距离相等．

查看试题解析
19. 如图，在平行四边形ABCD中，E、F分别在AD、BC边上，且AE=CF．
求证：

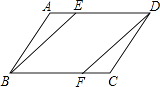(1)、△ABE≌△CDF；

(2)、四边形BFDE是平行四边形．

查看试题解析
20. 为创建“国家园林城市”，某校举行了以“爱我黄石”为主题的图片制作比赛，评委会对200名同学的参赛作品打分发现，参赛者的成绩x均满足50≤x＜100，并制作了频数分布直方图，如图．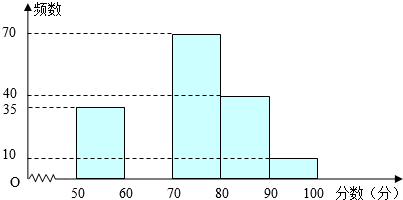

根据以上信息，解答下列问题：

(1)、请补全频数分布直方图；

(2)、若依据成绩，采取分层抽样的方法，从参赛同学中抽40人参加图片制作比赛总结大会，则从成绩80≤x＜90的选手中应抽多少人？

(3)、比赛共设一、二、三等奖，若只有25%的参赛同学能拿到一等奖，则一等奖的分数线是多少？

查看试题解析
21. 如图，有两棵树，一棵高10米，另一棵高4米，两树相距8米.一只小鸟从一棵树的树梢飞到另一棵树的树梢，问小鸟至少飞行多少米？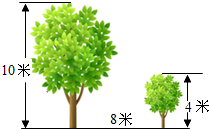

查看试题解析
22. 如图，在菱形ABCD中，AC ， BD相交于点O ， E为AB的中点，DE⊥AB ．

(1)、求∠ABC的度数；

(2)、如果AC＝4 $\sqrt{3}$ ，求DE的长．

查看试题解析
23.
如图，在Rt△ABC中，∠B=90°，AC=60cm，∠A=60°，点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（0＜t≤15）．过点D作DF⊥BC于点F，连接DE，EF．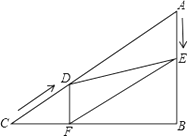

(1)、求证：AE=DF；

(2)、四边形AEFD能够成为菱形吗？如果能，求出相应的t值，如果不能，说明理由；

(3)、当t为何值时，△DEF为直角三角形？请说明理由．

查看试题解析

所剪次数	1	2	3	4	…	n
正三角形个数	4	7	10	13	…	a_n