四川省眉山市仁寿县龙正学区2018-2019学年八年级下学期数学期中考试试卷
试卷更新日期:2020-03-24 类型:期中考试
一、单选题
-
1. 在 , , , , ,中分式的个数有( )A、2个 B、3个 C、4个 D、5个2. 在平面直角坐标系中,若点P的坐标为(﹣3,2),则点P所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 对于函数y=2x﹣1,下列说法正确是( )A、它的图象过点(1,0) B、y值随着x值增大而减小 C、它的图象经过第二象限 D、当x>1时,y>04. 若分式 的值为0,则x的值为( )A、0 B、1 C、﹣1 D、±15. 下列各式变形正确是( )A、 B、 C、 D、6. 函数y= 自变量x的取值范围是( )A、x≥1 B、x≥1且x≠3 C、x≠3 D、1≤x≤37. 如图,函数y1=﹣2x 与 y2=ax+3 的图象相交于点 A(m,2),则关于 x 的不等式﹣2x>ax+3 的解集是( )
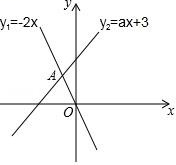 A、x>2 B、x<2 C、x>﹣1 D、x<﹣18. 关于x的方程 无解,则m的值为( )A、﹣5 B、﹣8 C、﹣2 D、59. 一次函数y=ax+b与反比例函数y= ,其中ab<0,a、b为常数,它们在同一坐标系中的图象可以是( )A、
A、x>2 B、x<2 C、x>﹣1 D、x<﹣18. 关于x的方程 无解,则m的值为( )A、﹣5 B、﹣8 C、﹣2 D、59. 一次函数y=ax+b与反比例函数y= ,其中ab<0,a、b为常数,它们在同一坐标系中的图象可以是( )A、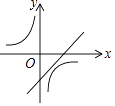 B、
B、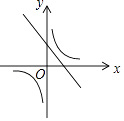 C、
C、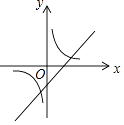 D、
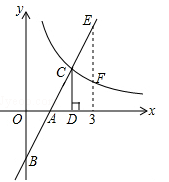
D、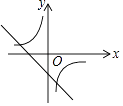 10. 如图,在直角坐标系中,直线 与坐标轴交于A、B两点,与双曲线 ( )交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:
10. 如图,在直角坐标系中,直线 与坐标轴交于A、B两点,与双曲线 ( )交于点C,过点C作CD⊥x轴,垂足为D,且OA=AD,则以下结论:① ;②当0<x<3时, ;③如图,当x=3时,EF= ;④当x>0时, 随x的增大而增大, 随x的增大而减小.其中符合题意结论的个数是( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 用科学记数法表示:0.0000002467= .12. 在平面直角坐标系中,把直线y=3x-3向上平移3个单位长度后,其直线解析式为13. 已知点M(3,2)与点N(x,y)在同一条平行于x轴的直线上,且点N到y轴的距离为5,则点N的坐标为 .14. 若分式 值为负,则x的取值范围是15. 若点A(a , 3a-b),B(b , 2a+b-2)关于x轴对称,则ab=16. 若直线y=3x+2不动,将平面直角坐标系xOy沿铅直方向向下平移5个单位,则平移后直线与y轴的交点坐标为17. 若 ,则 的值是 .18. 如图,在平面直角坐标系中,BA⊥y轴于点A , BC⊥x轴于点C , 函数 的图象分别交BA , BC于点D , E当AD:BD=1:3且 的面积为18时,则k的值是

三、解答题
-
19.(1)、计算:(2)、20. 先化简(1﹣ )÷ ,然后从﹣2≤a≤2的范围内选取一个合适的整数作为a的值代入求值.21. 已知关于x的方程 解为正数,求m的取值范围.22. 某校初一年学生乘车到距学校 千米的社会实践基地进行社会实践.一部分学生乘旅游车,另一部分学生乘中巴车,他们同时出发,结果乘中巴车的同学晚到 分钟.已知旅游车速度是中巴车速度的 倍,求中巴车的速度是多少千米/小时?23. 解方程(1)、(2)、24. 心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如下图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
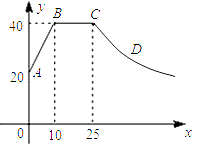 (1)、开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?(2)、一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?25. 如图,直线 与反比例函数 的图像交点A.点B,与x轴相交于点C,其中点A的坐标为(-2,4),点B的纵坐标为2.
(1)、开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?(2)、一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?25. 如图,直线 与反比例函数 的图像交点A.点B,与x轴相交于点C,其中点A的坐标为(-2,4),点B的纵坐标为2. (1)、当x为何值时,一次函数的值大于反比例函数的值.(直接写出来)(2)、求△AOB的面积.26. 健身运动已成为时尚,某公司计划组装A、B两种型号的健身器材共40套,捐给社区健身中心. 组装一套A型健身器材需甲种部件7个和乙种部件4个,组装一套B型健身器材需甲种部件3个和乙种部件6个.公司现有甲种部件240个,乙种部件196个.(1)、公司在组装A、B两种型号的健身器材时,共有多少种组装方案?(2)、组装一套A型健身器材需费用20元,组装一套B型健身器材需费用18元,求总组装费用最少的组装方案,最少总组装费用是多少?27. 如图,直线y=kx-1与x轴、y轴分别交于B、C两点,OB:OC= .
(1)、当x为何值时,一次函数的值大于反比例函数的值.(直接写出来)(2)、求△AOB的面积.26. 健身运动已成为时尚,某公司计划组装A、B两种型号的健身器材共40套,捐给社区健身中心. 组装一套A型健身器材需甲种部件7个和乙种部件4个,组装一套B型健身器材需甲种部件3个和乙种部件6个.公司现有甲种部件240个,乙种部件196个.(1)、公司在组装A、B两种型号的健身器材时,共有多少种组装方案?(2)、组装一套A型健身器材需费用20元,组装一套B型健身器材需费用18元,求总组装费用最少的组装方案,最少总组装费用是多少?27. 如图,直线y=kx-1与x轴、y轴分别交于B、C两点,OB:OC= . (1)、求B点的坐标和k的值.(2)、若点A(x , y)是第一象限内的直线y=kx-1上的一个动点,当点A运动过程中,试写出△AOB的面积S与x的函数关系式;(3)、在(2)的条件下,当点A运动到什么位置时,△AOB的面积是 .
(1)、求B点的坐标和k的值.(2)、若点A(x , y)是第一象限内的直线y=kx-1上的一个动点,当点A运动过程中,试写出△AOB的面积S与x的函数关系式;(3)、在(2)的条件下,当点A运动到什么位置时,△AOB的面积是 .