备考2020年中考数学二轮复习拔高训练卷 专题6 三角形
试卷更新日期:2020-03-23 类型:二轮复习
一、单选题
-
1. 如图是用8块A型瓷砖(白色四边形)和8块B型瓷砖(黑色三角形)不重叠、无空隙拼接而成的一个正方形图案,图案中A型瓷砖的总面积与B型瓷砖的总面积之比为( )
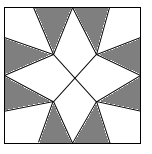 A、 :1 B、3:2 C、 :1 D、 :22. 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点O是AB的三等分点,半圆O与AC相切,M,N分别是BC与半圆弧上的动点,则MN的最小值和最大值之和是( )
A、 :1 B、3:2 C、 :1 D、 :22. 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点O是AB的三等分点,半圆O与AC相切,M,N分别是BC与半圆弧上的动点,则MN的最小值和最大值之和是( )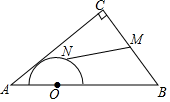 A、5 B、6 C、7 D、83. 如图,在 中,D在AC边上, ,O是BD的中点,连接AO并延长交BC于E,则 ( )
A、5 B、6 C、7 D、83. 如图,在 中,D在AC边上, ,O是BD的中点,连接AO并延长交BC于E,则 ( )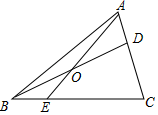 A、1:2 B、1:3 C、1:4 D、2:34. 如图,△ABC中,AB=AC=2,∠B=30°,△ABC绕点A逆时针旋转α(0<α<120°)得到 , 与BC,AC分别交于点D,E.设 , 的面积为 ,则 与 的函数图象大致为( )
A、1:2 B、1:3 C、1:4 D、2:34. 如图,△ABC中,AB=AC=2,∠B=30°,△ABC绕点A逆时针旋转α(0<α<120°)得到 , 与BC,AC分别交于点D,E.设 , 的面积为 ,则 与 的函数图象大致为( )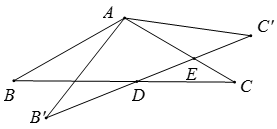 A、
A、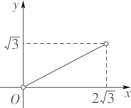 B、
B、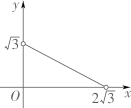 C、
C、 D、
D、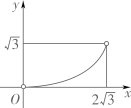 5. 如图,△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E , D是线段BE上的一个动点,则 的最小值是( )
5. 如图,△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E , D是线段BE上的一个动点,则 的最小值是( )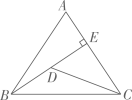 A、 B、 C、 D、106. 如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边DE上,若AE= ,AD= ,则两个三角形重叠部分的面积为( )
A、 B、 C、 D、106. 如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边DE上,若AE= ,AD= ,则两个三角形重叠部分的面积为( )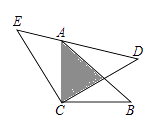 A、 B、 C、 D、7. 如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB=( )
A、 B、 C、 D、7. 如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,且∠ADC=110°,则∠MAB=( )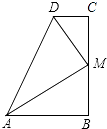 A、30° B、35° C、45° D、60°8. 如图, ,且 . 、 是 上两点, , .若 , , ,则 的长为( )
A、30° B、35° C、45° D、60°8. 如图, ,且 . 、 是 上两点, , .若 , , ,则 的长为( )
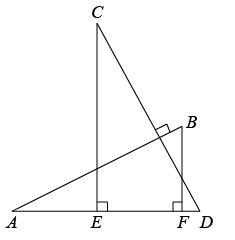 A、 B、 C、 D、9. 在 中, , 于 , 平分 交 于 ,则下列结论一定成立的是( )
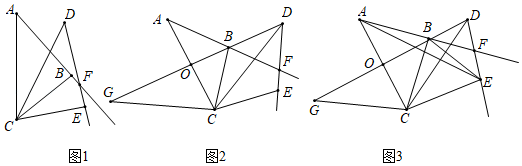
A、 B、 C、 D、9. 在 中, , 于 , 平分 交 于 ,则下列结论一定成立的是( )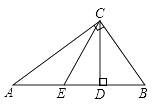 A、 B、 C、 D、10. 如图,等边三角形 边长是定值,点 是它的外心,过点 任意作一条直线分别交 , 于点 , ,将 沿直线 折叠,得到 ,若 , 分别交 于点 , ,连接 , ,则下列判断错误的是( )
A、 B、 C、 D、10. 如图,等边三角形 边长是定值,点 是它的外心,过点 任意作一条直线分别交 , 于点 , ,将 沿直线 折叠,得到 ,若 , 分别交 于点 , ,连接 , ,则下列判断错误的是( )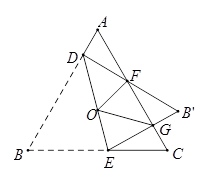 A、 B、 的周长是一个定值 C、四边形 的面积是一个定值 D、四边形 的面积是一个定值11. 如图,∠AOB=60°,点P是∠AOB内的定点且OP= ,若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是( )
A、 B、 的周长是一个定值 C、四边形 的面积是一个定值 D、四边形 的面积是一个定值11. 如图,∠AOB=60°,点P是∠AOB内的定点且OP= ,若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是( )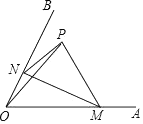 A、 B、 C、6 D、312. 如图,等边三角形 的边长为4,点 是△ 的中心, .绕点 旋转 ,分别交线段 于D、E两点,连接 ,给出下列四个结论:① ;② ;③四边形 的面积始终等于 ;④△ 周长的最小值为6,上述结论中正确的个数是( )
A、 B、 C、6 D、312. 如图,等边三角形 的边长为4,点 是△ 的中心, .绕点 旋转 ,分别交线段 于D、E两点,连接 ,给出下列四个结论:① ;② ;③四边形 的面积始终等于 ;④△ 周长的最小值为6,上述结论中正确的个数是( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
13. 如图, 是等边三角形,点D为BC边上一点, ,以点D为顶点作正方形DEFG,且 ,连接AE,AG.若将正方形DEFG绕点D旋转一周,当AE取最小值时,AG的长为.
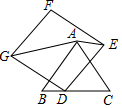 14. 图1是一种折叠式晾衣架.晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,两支脚OC=OD=10分米,展开角∠COD=60°,晾衣臂OA=OB=10分米,晾衣臂支架HG=FE=6分米,且HO=FO=4分米.当∠AOC=90°时,点A离地面的距离AM为分米;当OB从水平状态旋转到OB′(在CO延长线上)时,点E绕点F随之旋转至OB′上的点E′处,则B′E′﹣BE为分米.
14. 图1是一种折叠式晾衣架.晾衣时,该晾衣架左右晾衣臂张开后示意图如图2所示,两支脚OC=OD=10分米,展开角∠COD=60°,晾衣臂OA=OB=10分米,晾衣臂支架HG=FE=6分米,且HO=FO=4分米.当∠AOC=90°时,点A离地面的距离AM为分米;当OB从水平状态旋转到OB′(在CO延长线上)时,点E绕点F随之旋转至OB′上的点E′处,则B′E′﹣BE为分米.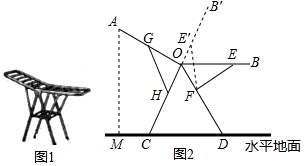 15. 如图,Rt△ABC中,∠C=90°,AC=12,点D在边BC上,CD=5,BD=13.点P是线段AD上一动点,当半径为6的OP与△ABC的一边相切时,AP的长为.
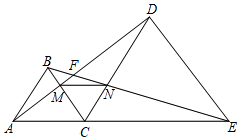
15. 如图,Rt△ABC中,∠C=90°,AC=12,点D在边BC上,CD=5,BD=13.点P是线段AD上一动点,当半径为6的OP与△ABC的一边相切时,AP的长为.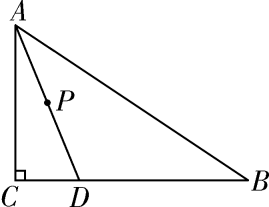 16. 如图, 和 都是等边三角形,且点A、C、E在同一直线上, 与 、 分别交于点F、M , 与 交于点N . 下列结论正确的是(写出所有正确结论的序号).
16. 如图, 和 都是等边三角形,且点A、C、E在同一直线上, 与 、 分别交于点F、M , 与 交于点N . 下列结论正确的是(写出所有正确结论的序号).① ;② ;③ ;④
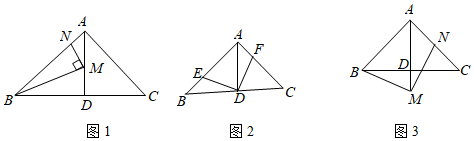
 17. 如图,在△ABC中,∠BAC=90°,AB=AC=10cm,点D为△ABC内一点,∠BAD=15°,AD=6cm,连接BD,将△ABD绕点A逆时针方向旋转,使AB与AC重合,点D的对应点E,连接DE,DE交AC于点F,则CF的长为cm.
17. 如图,在△ABC中,∠BAC=90°,AB=AC=10cm,点D为△ABC内一点,∠BAD=15°,AD=6cm,连接BD,将△ABD绕点A逆时针方向旋转,使AB与AC重合,点D的对应点E,连接DE,DE交AC于点F,则CF的长为cm. 18. 把两个同样大小含 角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个三角尺的直角顶点重合于点 ,且另外三个锐角顶点 在同一直线上.若 ,则 .
18. 把两个同样大小含 角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个三角尺的直角顶点重合于点 ,且另外三个锐角顶点 在同一直线上.若 ,则 .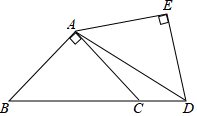 19. 如图,等边三角形ABC内有一点P,分別连结AP、BP、CP,若 , , .则 = .
19. 如图,等边三角形ABC内有一点P,分別连结AP、BP、CP,若 , , .则 = .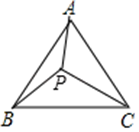
三、解答题
-
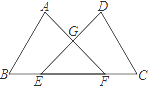
20. 如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C,AF与DE交于点G,求证:GE=GF.
 21. 已知:在△ABC中,AB=AC,D为AC的中点,DE⊥AB,DF⊥BC,垂足分别为点E,F,且DE=DF。
21. 已知:在△ABC中,AB=AC,D为AC的中点,DE⊥AB,DF⊥BC,垂足分别为点E,F,且DE=DF。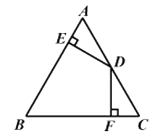
求证:△ABC是等边三角形。
四、综合题
-
22. 在Rt△ABC中,∠ACB=90°,D是△ABC内一点,连接AD,BD.在BD左侧作Rt△BDE,使∠BDE=90°,以AD和DE为邻边作▱ADEF,连接CD,DF.
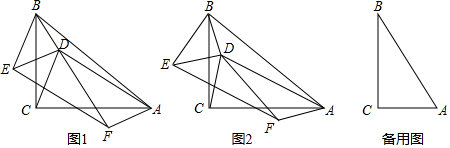 (1)、若AC=BC,BD=DE.
(1)、若AC=BC,BD=DE.①如图1,当B,D,F三点共线时,CD与DF之间的数量关系为.
②如图2,当B,D,F三点不共线时,①中的结论是否仍然成立?请说明理由.
(2)、若BC=2AC,BD=2DE, ,且E,C,F三点共线,求 的值.23. (1)、【思维启迪】
(1)、【思维启迪】如图1,A,B两点分别位于一个池塘的两端,小亮想用绳子测量A,B间的距离,但绳子不够长,聪明的小亮想出一个办法:先在地上取一个可以直接到达B点的点C,连接BC,取BC的中点P(点P可以直接到达A点),利用工具过点C作CD∥AB交AP的延长线于点D,此时测得CD=200米,那么A,B间的距离是米.
(2)、【思维探索】在△ABC和△ADE中,AC=BC,AE=DE,且AE<AC,∠ACB=∠AED=90°,将△ADE绕点A顺时针方向旋转,把点E在AC边上时△ADE的位置作为起始位置(此时点B和点D位于AC的两侧),设旋转角为α,连接BD,点P是线段BD的中点,连接PC,PE.①如图2,当△ADE在起始位置时,猜想:PC与PE的数量关系和位置关系分别是;
②如图3,当α=90°时,点D落在AB边上,请判断PC与PE的数量关系和位置关系,并证明你的结论;
③当α=150°时,若BC=3,DE=1,请直接写出PC2的值.