河南省南阳市2016-2017学年高二下学期理数期末考试试卷
试卷更新日期:2017-08-25 类型:期末考试
一、选择题
-
1. 已知:z(1+2i)=3﹣i,则 =( )A、 B、 C、 D、2. 设随机变量ξ~B(2,p),随机变量η~B(3,p),若 ,则Eη=( )A、 B、 C、1 D、3. 在如图所示的正方形中随机投掷10000个点,则落入阴影部分(曲线C为正态分布N(﹣1,1)的密度曲线在正方形內的部分)的点的个数的估计值为( )
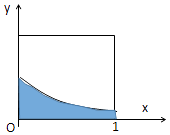 A、1193 B、1359 C、2718 D、34134. x,y的取值如表,从散点图分析,y与x线性相关,且回归方程为 ,则m=( )
A、1193 B、1359 C、2718 D、34134. x,y的取值如表,从散点图分析,y与x线性相关,且回归方程为 ,则m=( )x
1
2
3
4
5
y
2
7
8
12
m
A、15 B、16 C、16.2 D、175. 《聊斋志异》中有这样一首诗:“挑水砍柴不堪苦,请归但求穿墙术.得诀自诩无所阻,额上坟起终不悟.”在这里,我们称形如以下形式的等式具有“穿墙术”:2 = ,3 = ,4 = ,5 =
则按照以上规律,若8 = 具有“穿墙术”,则n=( )
A、7 B、35 C、48 D、636. 从混有3张假钞的10张百元钞票中任意抽出2张,将其中1张放到验钞机上检验发现是假钞,则另一张也是假钞的概率为( )A、 B、 C、 D、7. 函数f(x)= x﹣sinx(x∈R)的部分图象是( )A、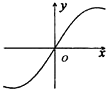 B、
B、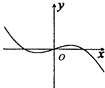 C、
C、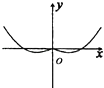 D、
D、 8. 已知函数函数 ,其中a>0,若函数f(x)在区间(﹣2,0)内恰好有两个零点,则实数a的取值范围是( )A、(0,3) B、(3,+∞) C、 D、9. 已知: ,则a6=( )A、﹣28 B、﹣448 C、112 D、44810. 已知数列{an}各项的绝对值均为1,Sn为其前n项和.若S7=3,则该数列{an}的前七项的可能性有( )种.A、10 B、20 C、21 D、4211. 若f(x)= ,则f(2017)=( )A、 B、 C、 D、12. 已知定义在R上函数f(x)是可导的,f(1)=2,且f(x)+f'(x)<1,则不等式f(x)﹣1<e1﹣x的解集是( )(注:e为自然对数的底数)A、(1,+∞) B、(﹣∞,0)∪(0,1) C、(0,1) D、(﹣∞,1)
8. 已知函数函数 ,其中a>0,若函数f(x)在区间(﹣2,0)内恰好有两个零点,则实数a的取值范围是( )A、(0,3) B、(3,+∞) C、 D、9. 已知: ,则a6=( )A、﹣28 B、﹣448 C、112 D、44810. 已知数列{an}各项的绝对值均为1,Sn为其前n项和.若S7=3,则该数列{an}的前七项的可能性有( )种.A、10 B、20 C、21 D、4211. 若f(x)= ,则f(2017)=( )A、 B、 C、 D、12. 已知定义在R上函数f(x)是可导的,f(1)=2,且f(x)+f'(x)<1,则不等式f(x)﹣1<e1﹣x的解集是( )(注:e为自然对数的底数)A、(1,+∞) B、(﹣∞,0)∪(0,1) C、(0,1) D、(﹣∞,1)二、填空题
-
13. 在二项式( + )n的展开式中,前三项的系数成等差数列,把展开式中所有的项重新排成一列,则有理项都不相邻的概率为 .14. 若函数f(x)=ex+ax2 无极值点,则a的取值范围是 .15. 已知结论:“在三边长都相等的△ABC中,若D是BC的中点,G是△ABC外接圆的圆心,则 ”.若把该结论推广到空间,则有结论:“在六条棱长都相等的四面体ABCD中,若M是△BCD的三边中线的交点,O为四面体ABCD外接球的球心,则 = .16. 已知函数f(x)的导函数为f'(x),且 ,则 = .
三、解答题:
-
17. 已知:二项式 展开式中所有项的 二项式系数和为64,(1)、求n的值;(2)、若展开式所有项的 系数和为 ,其中a,b为有理数,求a和b的值.18. 为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列表:
喜爱打篮球
不喜爱打篮球
合计
男生
20
5
25
女生
10
15
25
合计
30
20
50
(1)、用分层抽样的方法在喜欢打篮球的学生中抽6人,其中男生抽多少人?(2)、在上述抽取的6人中选2人,求恰有一名女生的概率.(3)、为了研究喜欢打篮球是否与性别有关,计算出K2 , 你有多大的把握认为是否喜欢打篮球与性别有关?附:
下面的临界值表供参考:
p(K2≥k)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828
19. (1)已知:x∈(0+∞),求证: ;20. 学校在军训过程中要进行打靶训练,给每位同学发了五发子弹,打靶规则:每个同学打靶过程中,若 连续两发命中或者 连续两发不中则要停止射击,否则将子弹打完.假设张同学在向目标射击时,每发子弹的命中率为 .(1)、求张同学前两发只命中一发的概率;(2)、求张同学在打靶过程中所耗用的子弹数X的分布列与期望.