西省赣州市2016-2017学年江高二下学期文数期末考试试卷
试卷更新日期:2017-08-25 类型:期末考试
一、选择题
-
1. 设集合M={﹣4,﹣3,﹣2,﹣1,0,1},N={x∈R|x2+3x<0},则M∩N=( )A、{﹣3,﹣2,﹣1,0} B、{﹣2,﹣1,0} C、{﹣3,﹣2,﹣1} D、{﹣2,﹣1}2. 下列函数中,满足“f(x+y)=f(x)f(y)”的单调递增函数是( )A、f(x)=x3 B、f(x)=x C、f(x)=3x D、f(x)=( )x3. 若a,b,c∈R,a>b,则下列不等式成立的是( )A、 B、a2>b2 C、a|c|>b|c| D、4. 曲线C的极坐标方程为ρ=6sinθ化为直角坐标方程后为( )A、x2+(y﹣3)2=9 B、x2+(y+3)2=9 C、(x+3)2+y2=9 D、(x﹣3)2+y2=95. 设a=log2 ,b=30.01 , c=ln ,则( )A、c<a<b B、a<b<c C、a<c<b D、b<a<c6. 定义集合运算:A⊙B={z︳z=xy(x+y),x∈A,y∈B},设集合A={0,1},B={2,3},则集合A⊙B的所有元素之和为( )A、0 B、6 C、12 D、187. 已知函数f(x)的定义域是[﹣1,1],则函数g(x)=f(2x﹣1)lg(1﹣x)的定义域是( )A、[0,1] B、(0,1) C、[0,1) D、(0,1]8. 若函数f(x)=|x+1|+|x+a|的最小值为3,则实数a的值为( )A、3 B、2 C、2或﹣4 D、4或﹣29. 在直角坐标系和以原点为极点,以x轴正方向为极轴建立的极坐标系中,直线l:y+kx+2=0与曲线C:ρ=2cosθ相交,则k的取值范围是( )A、k∈R B、k≥﹣ C、k<﹣ D、k∈R但k≠010. 设函数f(x)=log x+x﹣a,则“a∈(1,5)”是“函数f(x)在(2,8)上存在零点”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要11. 已知函数f(x)=sinx,x∈(0,2π),点P(x,y)是函数f(x)图象上任一点,其中0(0,0),A(2π,0),记△OAP的面积为g(x),则g′(x)的图象可能是( )A、
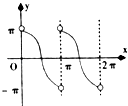 B、
B、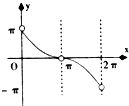 C、
C、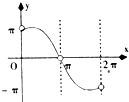 D、
D、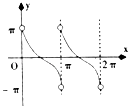 12. 已知定义在R上的函数f(x)满足:y=f(x﹣1)的图象关于(1,0)点对称,且当x≥0时恒有f(x+2)=f(x),当x∈[0,2)时,f(x)=ex﹣1,则f(2016)+f(﹣2017)=( )(其中e为自然对数的底)A、1﹣e B、e﹣1 C、﹣1﹣e D、e+1
12. 已知定义在R上的函数f(x)满足:y=f(x﹣1)的图象关于(1,0)点对称,且当x≥0时恒有f(x+2)=f(x),当x∈[0,2)时,f(x)=ex﹣1,则f(2016)+f(﹣2017)=( )(其中e为自然对数的底)A、1﹣e B、e﹣1 C、﹣1﹣e D、e+1二、填空题
-
13. 已知函数f(x)= ,则f(f(4))= .14. 在极坐标系中,O是极点,设点A(1, ),B(2, ),则△OAB的面积是 .15. 直线x=a(a>0)分别与直线y=3x+3,曲线y=2x+lnx交于A、B两点,则|AB|最小值为 .16. 太极图是由黑白两个鱼形纹组成的图案,俗称阴阳鱼,太极图展现了一种相互转化,相互统一的和谐美.定义:能够将圆O的周长和面积同时等分成两部分的函数称为圆煌一个“太极函数”下列有关说法中:

①对圆O:x2+y2=1的所有非常数函数的太极函数中,一定不能为偶函数;
②函数f(x)=sinx+1是圆O:x2+(y﹣1)2=1的一个太极函数;
③存在圆O,使得f(x)= 是圆O的太极函数;
④直线(m+1)x﹣(2m+1)y﹣1=0所对应的函数一定是圆O:(x﹣2)2+(y﹣1)2=R2(R>0)的太极函数.
所有正确说法的序号是 .
三、解答题
-
17. 已知函数f(x)=ex﹣ax+b.(1)、若f(x)在x=2有极小值1﹣e2 , 求实数a,b的值.(2)、若f(x)在定义域R内单调递增,求实数a的取值范围.18. 已知函数f(x)=m﹣|x﹣2|,m∈R,且f(x+2)≥0的解集为[﹣1,﹣1].(1)、求m的值;(2)、若a,b,c∈R,且 + + =m,求证:a2+b2+c2≥36.19. 设命题p:实数x满足|x﹣1|>a其中a>0;命题q:实数x满足 <1(1)、若命题p中a=1,且p∧q为真,求实数x的取值范围;(2)、若¬p是q的必要不充分条件,求实数a的取值范围.20. 在平面直角坐标系xOy中,已知直线l: (t为参数)与圆C: (θ为参数)相交于A,B两点.(1)、求直线l及圆C的普通方程(2)、已知F(1,0),求|FA|+|FB|的值.