四川省资阳市2016-2017学年高二下学期文数期末考试试卷
试卷更新日期:2017-08-25 类型:期末考试
一、选择题
-
1. 已知i是虚数单位,若复数z满足:z(1﹣i)=2,则复数z=( )A、﹣1﹣i B、1﹣i C、﹣1+i D、1+i2. 抛物线y2=2x的焦点坐标为( )A、(0, ) B、(0,1) C、( ,0) D、(1,0)3. 以平面直角坐标原点为极点,x轴正半轴为极轴,则直角坐标为(﹣2,2)的点的极坐标为( )A、(2 , ) B、(2 , ) C、(2, ) D、(2, )4. 若双曲线 的一条渐近线方程为y=2x,则离心率e=( )A、 B、 C、 D、5. 设f′(x)是函数f(x)的导函数,y=f′(x)的图象如图所示,则y=f(x)的图象最有可能的是( )
 A、
A、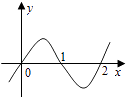 B、
B、 C、
C、 D、
D、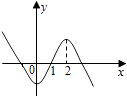 6. 某公司奖励甲,乙,丙三个团队去A,B,C三个景点游玩,三个团队各去一个不同景点,征求三个团队意见得到:甲团队不去A;乙团队不去B;丙团队只去A或C.公司按征求意见安排,则下列说法一定正确的是( )A、丙团队一定去A景点 B、乙团队一定去C景点 C、甲团队一定去B景点 D、乙团队一定去A景点7. 曲线C的参数方程为 (θ是参数),则曲线C的形状是( )A、线段 B、直线 C、射线 D、圆8. 根据如下样本数据:
6. 某公司奖励甲,乙,丙三个团队去A,B,C三个景点游玩,三个团队各去一个不同景点,征求三个团队意见得到:甲团队不去A;乙团队不去B;丙团队只去A或C.公司按征求意见安排,则下列说法一定正确的是( )A、丙团队一定去A景点 B、乙团队一定去C景点 C、甲团队一定去B景点 D、乙团队一定去A景点7. 曲线C的参数方程为 (θ是参数),则曲线C的形状是( )A、线段 B、直线 C、射线 D、圆8. 根据如下样本数据:x
3
4
5
6
7
y
4.0
2.5
0.5
﹣0.5
﹣2.0
得到的回归方程为 =bx+a.若a=8.4,则估计x,y的变化时,若x每增加1个单位,则y就( )
A、增加1.2个单位 B、减少1.5个单位 C、减少2个单位 D、减少1.2个单位9. 若f(x)的定义域为R,f′(x)>3恒成立,f(1)=9,则f(x)>3x+6解集为( )A、(﹣1,1) B、(﹣1,+∞) C、(﹣∞,﹣1) D、(1.+∞)10. 已知过点M(2,0)的动直线l交抛物线y2=2x于A,B两点,则 • 的值为( )A、2 B、0 C、4 D、﹣211. 已知抛物线C:y2=4x焦点为F,点D为其准线与x轴的交点,过点F的直线l与抛物线相交于A,B两点,则△DAB的面积S的取值范围为( )A、[5,+∞) B、[2,+∞) C、[4,+∞) D、[2,4]12. 若对∀x∈[0,+∞),不等式2ax≤ex﹣1恒成立,则实数a的最大值是( )A、 B、 C、1 D、2二、填空题
-
13. 曲线f(x)=ex+x+1在点(0,f(0))处的切线方程为 .14. 直线 (t为参数)与圆 (θ为参数)的位置关系是 .15. 已知函数f(x)的导函数为f′(x),且f(x)=2xf′(1)+lnx,则f′(1)= .16. 直线l1 , l2分别是函数f(x)=sinx,x∈[0,π]图象上点P1 , P2处的切线,l1 , l2垂直相交于点P,且l1 , l2分别与y轴相交于点A,B,则△PAB的面积为 .
三、解答题
-
17. 在直角坐标平面内,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程是ρ=4sinθ,直线l的参数方程是 (t为参数).(1)、求直线l的普通方程和曲线C的直角坐标方程;(2)、求曲线C上的点到直线l的距离的最大值.18. 分别根据下列条件,求双曲线的标准方程.(1)、右焦点为 ,离心率e= ;(2)、实轴长为4的等轴双曲线.19. 已知函数f(x)=x+ ﹣3lnx(a∈R).(1)、若x=3是f(x)的一个极值点,求a值及f(x)的单调区间;(2)、当a=﹣2时,求f(x)在区间[1,e]上的最值.20. 为做好2022年北京冬季奥运会的宣传工作,组委会计划从某大学选取若干大学生志愿者,某记者在该大学随机调查了1000名大学生,以了解他们是否愿意做志愿者工作,得到的数据如表所示:
愿意做志愿者工作
不愿意做志愿者工作
合计
男大学生
610
女大学生
90
合计
800
(1)、根据题意完成表格;(2)、是否有95%的把握认为愿意做志愿者工作与性别有关?参考公式及数据: ,其中n=a+b+c+d.
P(K2≥K0)
0.25
0.15
0.10
0.05
0.025
K0
1.323
2.072
2.706
3.841
5.024