四川省资阳市2016-2017学年高二下学期理数期末考试试卷
试卷更新日期:2017-08-25 类型:期末考试
一、选择题
-
1. 某同学投篮命中率为0.6,则该同学1次投篮时命中次数X的期望为( )A、0.4 B、0.36 C、0.16 D、0.62. 设i为虚数单位,复数z满足z(1﹣i)=2i,则复数z=( )A、﹣1+i B、﹣1﹣i C、1﹣i D、1+i3. 若双曲线 的一条渐近线方程为y=2x,则离心率e=( )A、 B、 C、 D、4. 已知函数f(x)的导函数为f′(x),且满足f(x)=3xf'(1)+lnx,则f′(1)=( )A、﹣ B、 C、﹣1 D、e5. 若从1,2,3,4,5,6,7这7个整数中同时取3个不同的数,其和为奇数,则不同的取法共有( )A、10种 B、15种 C、16种 D、20种6. 设f′(x)是函数f(x)的导函数,y=f′(x)的图象如图所示,则y=f(x)的图象最有可能的是( )
 A、
A、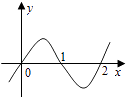 B、
B、 C、
C、 D、
D、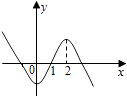 7. 已知X的分布列为:
7. 已知X的分布列为:X
﹣1
0
1
P
设Y=2X+3,则Y的期望E(Y)=( )
A、3 B、1 C、0 D、48. 设(1+x)n=a0+a1x+a2x2+…+anxn , 若a1+a2+…+an=63,则展开式中系数最大项是( )A、20 B、20x3 C、105 D、105x49. 若f(x)的定义域为R,f′(x)>3恒成立,f(1)=9,则f(x)>3x+6解集为( )A、(﹣1,1) B、(﹣1,+∞) C、(﹣∞,﹣1) D、(1.+∞)10. 已知抛物线C:y2=4x焦点为F,点D为其准线与x轴的交点,过点F的直线l与抛物线相交于A,B两点,则△DAB的面积S的取值范围为( )A、[5,+∞) B、[2,+∞) C、[4,+∞) D、[2,4]11. 已知对∀x∈(0,+∞),不等式2ax>ex﹣1恒成立,则实数a的最小值是( )A、2 B、1 C、 D、12. 袋中装有编号分别为1,2,3,…,2n的2n(n∈N*)个小球,现将袋中的小球分给A,B,C三个盒子,每次从袋中任意取出两个小球,将其中一个放入A盒子,如果这个小球的编号是奇数,就将另一个放入B盒子,否则就放入C盒子,重复上述操作,直到所有小球都被放入盒中,则下列说法一定正确的是( )A、B盒中编号为奇数的小球与C盒中编号为偶数的小球一样多 B、B盒中编号为偶数的小球不多于C盒中编号为偶数的小球 C、B盒中编号为偶数的小球与C盒中编号为奇数的小球一样多 D、B盒中编号为奇数的小球多于C盒中编号为奇数的小球二、填空题
-
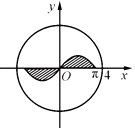
13. 曲线f(x)=ex+x+1在点(0,f(0))处的切线方程为 .14. (x2﹣ )6的展开式中x3的系数为 .15. 如图,圆O:x2+y2=16内的正弦曲线y=sinx,x∈[﹣π,π]与x轴围成的区域记为M(图中阴影部分),随机向圆O内投一个点P,记A表示事件“点P落在一象限”,B表示事件“点P落在区域M内”,则概率P(B|A)= .
 16. 直线l1 , l2分别是函数f(x)=sinx,x∈[0,π]图象上点P1 , P2处的切线,l1 , l2垂直相交于点P,且l1 , l2分别与y轴相交于点A,B,则△PAB的面积为 .
16. 直线l1 , l2分别是函数f(x)=sinx,x∈[0,π]图象上点P1 , P2处的切线,l1 , l2垂直相交于点P,且l1 , l2分别与y轴相交于点A,B,则△PAB的面积为 .三、解答题
-
17. 分别根据下列条件,求双曲线的标准方程.(1)、右焦点为 ,离心率e= ;(2)、实轴长为4的等轴双曲线.18. 已知某智能手机制作完成之后还需要依次通过三道严格的审核程序,已知第一道审核、第二道审核、第三道审核通过的概率分别为 , , ,每道程序是相互独立的,且一旦审核不通过就停止审核,每部手机只有三道程序都通过才能出厂销售.(1)、求审核过程中只进行两道程序就停止审核的概率;(2)、现有3部该智能手机进入审核,记这3部手机可以出厂销售的部数为X,求X的分布列及数学期望.19. 已知函数f(x)=x+ ﹣3lnx(a∈R).(1)、若x=3是f(x)的一个极值点,求a值及f(x)的单调区间;(2)、当a=﹣2时,求f(x)在区间[1,e]上的最值.20. 当今信息时代,众多高中生也配上了手机.某校为研究经常使用手机是否对学习成绩有影响,随机抽取高三年级50名理科生的一次数学周练成绩,并制成下面的2×2列联表:
及格
不及格
合计
很少使用手机
20
6
26
经常使用手机
10
14
24
合计
30
20
50
(1)、判断是否有97.5%的把握认为经常使用手机对学习成绩有影响?(2)、从这50人中,选取一名很少使用手机的同学记为甲和一名经常使用手机的同学记为乙,解一道数学题,甲、乙独立解出此题的概率分别为P1 , P2 , 且P2=0.5,若|P1﹣P2|≥0.4,则此二人适合结为学习上互帮互助的“学习师徒”,记X为两人中解出此题的人数,若X的数学期望E(X)=1.4,问两人是否适合结为“学习师徒”?参考公式及数据: ,其中n=a+b+c+d.
P(K2≥K0)
0.10
0.05
0.025
0.010
K0
2.706
3.841
5.024
6.635