湖北省宜昌市七校教学协作体2016-2017学年高二下学期文数期末考试试卷

试卷更新日期：2017-08-25 类型：期末考试

进入出卷网下载

一、选择题

1. 如果复数z= $\frac{2}{- 1 + i}$ ，则（）

A、|z|=2 B、z的实部为1 C、z的虚部为﹣1 D、z的共轭复数为1+i

查看试题解析
2. 将曲线y=sin 2x按照伸缩变换 ${\begin{matrix} x' = 2 x \\ y' = 3 y \end{matrix}$ 后得到的曲线方程为（）

A、y′=3sin 2x B、y′=3sin x′ C、y′=3sin $\frac{1}{2}$ x′ D、y′= $\frac{1}{3}$ sin 2x′

查看试题解析
3. 已知a＞b，c＞d，且c，d不为0，那么下列不等式一定成立的是（）

A、ad＞bc B、ac＞bd C、a﹣c＞b﹣d D、a+c＞b+d

查看试题解析
4. 在区间[﹣1，2]上随机取一个数x，则|x|≤1的概率为（）

A、 $\frac{2}{3}$ B、 $\frac{1}{4}$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
5. 抛物线y= $\frac{1}{8}$ x²的准线方程为（）

A、 $y = - \frac{1}{32}$ B、y=﹣2 C、x=﹣2 D、x=﹣ $\frac{1}{32}$

查看试题解析
6. 某学校组织学生参加英语测试，成绩的频率分布直方图如图，数据的分组依次为[20，40），[40，60），[60，80），[80，100]，若低于60分的人数是15人，则该班的学生人数是（）

A、45 B、50 C、55 D、60

查看试题解析
7. 下列说法正确的是（）

A、“p∨q”是“p∧q”的充分不必要条件 B、样本10，6，8，5，6的标准差是3.3 C、K²是用来判断两个分类变量是否相关的随机变量，当K²的值很小时可以推定两类变量不相关 D、设有一个回归直线方程为 $\hat{y}$ =2﹣1.5x，则变量x每增加一个单位， $\hat{y}$ 平均减少1.5个单位．

查看试题解析
8. 宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题：松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等．下图是源于其思想的一个程序框图，若输入的a，b分别为5，2，则输出的n=（）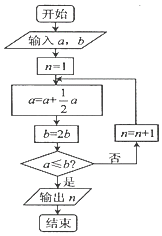

A、2 B、3 C、4 D、5

查看试题解析
9. 函数f（x）= $\frac{l n x - 2 x}{x}$ 的图象在点（1，﹣2）处的切线方程为（）

A、2x﹣y﹣4=0 B、2x+y=0 C、x﹣y﹣3=0 D、x+y+1=0

查看试题解析
10. 若函数f（x）=x+ $\frac{1}{x - 2}$ （x＞2），在x=a处取最小值，则a=（）

A、1+ $\sqrt{2}$ B、1+ $\sqrt{3}$ C、3 D、4

查看试题解析
11. 已知点M为椭圆 $\frac{x^{2}}{9}$ + $\frac{y^{2}}{4}$ =1上的点，则M到直线x+2y﹣10=0的距离的最小值是（）

A、 $\frac{7 \sqrt{5}}{5}$ B、 $\frac{6 \sqrt{5}}{5}$ C、 $\sqrt{5}$ D、2

查看试题解析
12. 《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土，这是我国现存最早的有系统的数学典籍，其中记载有求“囷盖”的术：置如其周，令相乘也，又以高乘之，三十六成一，该术相当于给出了由圆锥的底面周长L与高h，计算其体积V的近似公式V≈ $\frac{1}{36}$ L²h，它实际上是将圆锥体积公式中的圆周率π近似取为3，那么，近似公式V≈ $\frac{2}{75}$ L²h相当于将圆锥体积公式中的π近似取为（）

A、 $\frac{22}{7}$ B、 $\frac{25}{8}$ C、 $\frac{157}{50}$ D、 $\frac{355}{113}$

查看试题解析
13. 如图，椭圆 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ （a＞b＞0）的左、右顶点分别是A，B，左、右焦点分别是F₁ ， F₂ ，若|AF₁|，|F₁F₂|，|F₁B|成等比数列，则此椭圆的离心率为（）

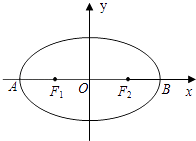A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{\sqrt{5}}{5}$ D、 $\sqrt{5} - 2$

查看试题解析
14. 给出定义：设f′（x）是函数y=f（x）的导函数，f″（x）是函数f′（x）的导函数，若方程f″（x）=0有实数解x₀ ，则称点（x₀ ， f（x₀））为函数y=f（x）的“拐点”．已知函数f（x）=3x+4sinx﹣cosx的拐点是M（x₀ ， f（x₀）），则点M（）

A、在直线y=﹣3x上 B、在直线y=3x上 C、在直线y=﹣4x上 D、在直线y=4x上

查看试题解析

二、填空题

15. 已知x和y之间的一组数据，若x、y具有线性相关关系，且回归方程为 $\hat{y}$ =x+a，则a的值为．
x
0
1
2
3
y
1
3
5
7

查看试题解析
16. 过点P（2，3），并且在两轴上的截距相等的直线方程为．

查看试题解析
17. 函数f（x）=x³﹣3x²+1在x₀处取得极小值，则x₀= ．

查看试题解析
18. 已知抛物线y²=2px的焦点F与双曲线 $\frac{x^{2}}{7}$ ﹣ $\frac{y^{2}}{9}$ =1的右焦点重合，抛物线的准线与x轴的焦点为K，点A在抛物线上，且|AK|= $\sqrt{2}$ |AF|，则△AFK的面积为．

查看试题解析

三、解答题

19. 已知直线l：x﹣2y﹣5=0，圆C：x²+y²=25．
（Ⅰ）求直线与圆C的交点A，B的坐标；
（Ⅱ）求△ABC的面积．

查看试题解析
20. 已知命题p：∀x∈[0，1]，a≥e^x ，命题q：“∃x∈R，x²+4x+a=0”，若命题“p∧q”是真命题，则实数a的取值范围是．

查看试题解析
21. 性格色彩学创始人乐嘉是江苏电视台当红节目“非诚勿扰”的特约嘉宾，他的点评视角独特，语言犀利，给观众留下了深刻的印象，某报社为了了解观众对乐嘉的喜爱程度，随机调查了观看了该节目的140名观众，得到如下的列联表：（单位：名）
男
女
总计
喜爱
40
60
100
不喜爱
20
20
40
总计
60
80
140
（Ⅰ）从这60名男观众中按对乐嘉是否喜爱采取分层抽样，抽取一个容量为6的样本，问样本中喜爱与不喜爱的观众各有多少名？
（Ⅱ）根据以上列联表，问能否在犯错误的概率不超过0.025%的前提下认为观众性别与喜爱乐嘉有关．（精确到0.001）
（Ⅲ）从（Ⅰ）中的6名男性观众中随机选取两名作跟踪调查，求选到的两名观众都喜爱乐嘉的概率．
附：
p（k²≥k₀）
0.10
0.05
0.025
0.010
0.005
k₀
2.705
3.841
5.024
6.635
7.879
k²= $\frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ．

查看试题解析
22. 在平面直角坐标系中，以坐标原点为极点，x轴的非负半轴为极轴建立极坐标系，已知点A的极坐标为（ $\sqrt{2}$ ， $\frac{π}{4}$ ），直线l的极坐标方程为ρcos（θ﹣ $\frac{π}{4}$ ）=a，且点A在直线l上，

(1)、求a的值及直线l的直角坐标方程；

(2)、圆C的参数方程为 ${\begin{matrix} x = 1 + c o s α \\ y = s i n α \end{matrix}$ （α为参数），试判断直线l与圆C的位置关系．

查看试题解析
23. 设函数f（x）=|3x﹣1|+ax+3
（Ⅰ）若a=1，解不等式f（x）≤4；
（Ⅱ）若函数f（x）有最小值，求a的取值范围．

查看试题解析
24. 已知椭圆E的右焦点与抛物线y²=4x的焦点重合，点M $(1 ， \frac{3}{2})$ 在椭圆E上．
（Ⅰ）求椭圆E的标准方程；
（Ⅱ）设P（﹣4，0），直线y=kx+1与椭圆E交于A，B两点，若∠APO=∠BPO，（其中O为坐标原点），
求k的值．

查看试题解析
25. 已知f（x）=xlnx，g（x）=x³+ax²﹣x+2．

(1)、求函数f（x）的单调区间；

(2)、对任意x∈（0，+∞），2f（x）≤g′（x）+2恒成立，求实数a的取值范围．

查看试题解析

p（k²≥k₀）	0.10	0.05	0.025	0.010	0.005
k₀	2.705	3.841	5.024	6.635	7.879

	男	女	总计
喜爱	40	60	100
不喜爱	20	20	40
总计	60	80	140