浙教版数学七年级上册第6章 6.7角的和差 同步练习
试卷更新日期：2017-08-25 类型：同步测试
一、单选题
-
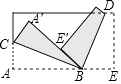
1. 将一长方形纸片，按图中的方式折叠，BC、BD为折痕，折叠后点E′刚好落在A′B上，则∠CBD的度数为（ ）
A、60° B、75° C、90° D、95°2. 如图，将长方形纸片ABCD的角C沿着GF折叠（点F在BC上，不与B，C重合），使点C落在长方形内部点E处，若FH平分∠BFE，则∠GFH的度数α是（ ）
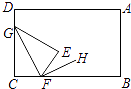A、90°＜α＜180° B、0°＜α＜90° C、α=90° D、α随折痕GF位置的变化而变化3. 已知∠AOB=50°，∠COB=30°，则∠AOC等于（ ）A、80° B、20° C、80°或20° D、无法确定4. 在15°、65°、75°、135°的角中，能用一副三角尺画出来的有（ ）A、1个 B、2个 C、3个 D、4个二、填空题
-
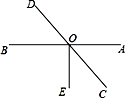
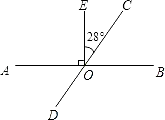
5. 如图，已知AB、CD相交于点O，OE⊥AB，∠EOC=28°，则∠AOD=度．
6. 把一张纸各按图中那样折叠后，若得到∠AOB′=70°，则∠B′OG=度．
7. 如图，将一副直角三角板叠在一起，使直角顶点重合于点0，则∠AOB=155°，则∠COD= ， ∠BOC= ．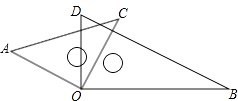
8. 从O点引三条射线OA、OB、OC，若∠AOB=120°，且∠AOC=∠BOC，则∠BOC= ．9. 如图，∠AOC=30°35′15″，∠BOC=80°15′28″，OC平分∠AOD，那么∠BOD等于 ．
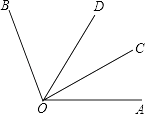10. 如图，已知∠AOD=90°，∠BOD=2∠AOB，OD平分∠BOC，则∠AOC=度．
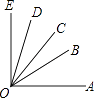
11. 如图所示，∠AOE=90°，∠BOD=45°，那么不大于90°的所有角的度数之和是度．
三、解答题
-
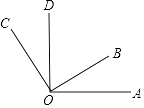
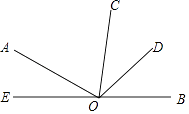
12. 如图，O为直线BE上的一点，∠AOE=36°，OC平分∠AOB，OD平分∠BOC，求∠AOD的度数．
13. 已知：OA⊥OC，∠AOB：∠AOC=2：3，画出图形，并求∠BOC的度数．14. 如图所示，直线AB、CD、EF交于点O，OG平分∠BOF，且CD⊥EF，∠AOE=70°，求∠DOG的度数．
15. 如图，直线AB、CD相交于O点，∠AOC与∠AOD的度数比为4：5，OE⊥AB，OF平分∠DOB，求∠EOF的度数．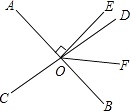
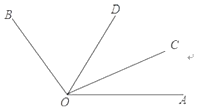
16.如图，已知∠AOC：∠BOC=1：4，OD平分∠AOB，且∠COD=36°，求∠AOB的度数．
17. 已知∠AOB=90°，OC是从∠AOB的顶点O引出的一条射线，若∠AOB=2∠BOC，求∠AOC的度数．18. 如图，将书角斜折过去，使角顶点落在A′处，BC为折痕，∠A′BD=∠DBE，求∠CBD的度数．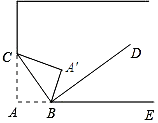
19. 如图，已知∠COB=2∠AOC，OD平分∠AOB，∠AOC=20°，求∠COD的度数．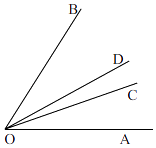
四、综合题
-
20. 如图，已知OM平分∠AOC，ON平分∠BOC，∠AOB=90°，∠BOC=30°．
求：
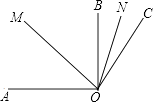(1)、∠AOC的度数；(2)、∠MON的度数．
