初中数学浙教版八年级下册第四章 平行四边形 章末检测
试卷更新日期:2020-03-20 类型:单元试卷
一、单选题
-
1. 下列图形中,即是轴对称图形又是中心对称图形的是( )A、
 B、
B、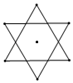 C、
C、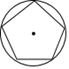 D、
D、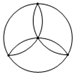 2. 已知一个多边形的内角和为540°,则这个多边形为( )A、三角形 B、四边形 C、五边形 D、六边形3. 在▱ABCD中,∠C、∠D的度数之比为3∶1,则 ∠A等于( )A、45° B、50° C、135° D、130°4. 在面积为12的平行四边形ABCD中,过点A作直线BC的垂线交直线BC于点E,过点A作直线CD的垂线交直线CD于点F,若AB=4,BC=6,则CE+CF的值为( )A、 B、 C、 或 D、 或5. 如图,在▱ABCD中,下列结论不一定成立的是( )
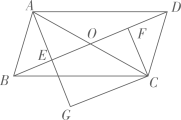
2. 已知一个多边形的内角和为540°,则这个多边形为( )A、三角形 B、四边形 C、五边形 D、六边形3. 在▱ABCD中,∠C、∠D的度数之比为3∶1,则 ∠A等于( )A、45° B、50° C、135° D、130°4. 在面积为12的平行四边形ABCD中,过点A作直线BC的垂线交直线BC于点E,过点A作直线CD的垂线交直线CD于点F,若AB=4,BC=6,则CE+CF的值为( )A、 B、 C、 或 D、 或5. 如图,在▱ABCD中,下列结论不一定成立的是( ) A、∠1=∠2 B、AD=DC C、∠ADC=∠CBA D、OA=OC6. A,B,C,D在同一平面内,从①AB∥CD;②AB=CD;③BC=AD;④BC∥AD这四个条件中任选两个,能使四边形ABCD是平行四边形的选法有( )A、3种 B、4种 C、5种 D、6种7. 小敏不慎将一块平行四边形玻璃打碎成如图所示的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,她带了两块碎玻璃,其编号应该是( )
A、∠1=∠2 B、AD=DC C、∠ADC=∠CBA D、OA=OC6. A,B,C,D在同一平面内,从①AB∥CD;②AB=CD;③BC=AD;④BC∥AD这四个条件中任选两个,能使四边形ABCD是平行四边形的选法有( )A、3种 B、4种 C、5种 D、6种7. 小敏不慎将一块平行四边形玻璃打碎成如图所示的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,她带了两块碎玻璃,其编号应该是( )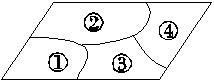 A、①② B、①④ C、③④ D、②③8. 如图,平行四边形ABCD中,E,F分别是AD,BC的中点,P是边DC上的动点,G,H分别是PE,PF的中点,已知DC=10cm,则GH的长是( )
A、①② B、①④ C、③④ D、②③8. 如图,平行四边形ABCD中,E,F分别是AD,BC的中点,P是边DC上的动点,G,H分别是PE,PF的中点,已知DC=10cm,则GH的长是( ) A、7cm B、6cm C、5cm D、4cm9. 命题“△ABC中,若∠A>∠B,则a>b”的结论的否定应该是( )A、a<b B、a≤b C、a=b D、a≥b10. 如图,在▱ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是( )
A、7cm B、6cm C、5cm D、4cm9. 命题“△ABC中,若∠A>∠B,则a>b”的结论的否定应该是( )A、a<b B、a≤b C、a=b D、a≥b10. 如图,在▱ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是( ) A、2 B、1 C、 D、
A、2 B、1 C、 D、二、填空题
-
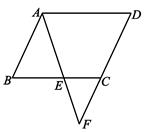
11. 八边形从其中的任何一个顶点最多可画条对角线,这些对角线可将八边形分成三角形.12. 如图,E是 ABCD边BC上一点,连结AE , 并延长AE与DC的延长线交于点F , 若AB=AE , ∠F =50°,则∠D=°.
 13. 在平面直角坐标系xOy中,若点B与点A(-2,3) 关于点O中心对称,则点B 的坐标为.14. 在平面直角坐标系xOy中,▱OABC的三个顶点O(0,0)、A(3,0) 、 B(4,2),则其第四个顶点是.15. 用反证法证明“若|a|<2,则a2<4”时,应假设 .16. 如图,四边形ABCD的边AB,BC,CD,DA的中点分别为E,F,G,H,则线段GE与线段HF的关系是.
13. 在平面直角坐标系xOy中,若点B与点A(-2,3) 关于点O中心对称,则点B 的坐标为.14. 在平面直角坐标系xOy中,▱OABC的三个顶点O(0,0)、A(3,0) 、 B(4,2),则其第四个顶点是.15. 用反证法证明“若|a|<2,则a2<4”时,应假设 .16. 如图,四边形ABCD的边AB,BC,CD,DA的中点分别为E,F,G,H,则线段GE与线段HF的关系是.
三、解答题
-
17. 如图,四边形 是平行四边形, 、 在对角线 上,且 ,连接 , , , .求证 .
 18. 已知:如图,△ABC的中线BD, CE交于点O,F,G分别是OB,OC的中点.求证:四边形DEFG是平行四边形.
18. 已知:如图,△ABC的中线BD, CE交于点O,F,G分别是OB,OC的中点.求证:四边形DEFG是平行四边形.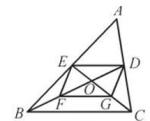 19. 如图,下列4×4网格图都是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在空白小正方形中,按下列要求涂上阴影.
19. 如图,下列4×4网格图都是由16个相同小正方形组成,每个网格图中有4个小正方形已涂上阴影,请在空白小正方形中,按下列要求涂上阴影.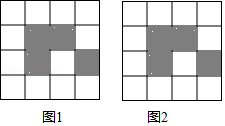 (1)、在图1中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个中心对称图形;(2)、在图2中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个轴对称图形,但不是中心对称图形.20.
(1)、在图1中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个中心对称图形;(2)、在图2中选取2个空白小正方形涂上阴影,使6个阴影小正方形组成一个轴对称图形,但不是中心对称图形.20.
(1)、如图是一个多边形,你能否用一直线去截这个多边形,使得到的新多边形分别满足下列条件:(画出图形,把截去的部分打上阴影)
①新多边形内角和比原多边形的内角和增加了180°.
②新多边形的内角和与原多边形的内角和相等.
③新多边形的内角和比原多边形的内角和减少了180°.
(2)、将多边形只截去一个角,截后形成的多边形的内角和为2520°,求原多边形的边数.21. 如图,▱ABCD中, 的角平分线 交AD于点E, 的角平分线 交 于点 , ,DE=3, =50°. (1)、求 的度数;(2)、求▱ABCD的周长.22. 锐角三角形ABC中,AC>BC,点D是边AC的中点,点E在边AB上.
(1)、求 的度数;(2)、求▱ABCD的周长.22. 锐角三角形ABC中,AC>BC,点D是边AC的中点,点E在边AB上.
①如果DE∥BC,那么DE= BC.
②如果DE= BC,那么DE∥BC.
判断上述两个命题是否成立,若成立,请说明理由;若不成立,请举出反例.