初中数学浙教版八年级下册4.4 平行四边形的判定(1） 同步训练

试卷更新日期：2020-03-20 类型：同步测试

进入 出卷网 下载

一、基础夯实

  • 1. 在四边形ABCD中，∠A：∠B：∠C：∠D的比例依次如下，其中能使四边形ABCD是平行四边形的是（ ）
    A、1：2：3：4 B、2：2：3：3 C、2：3：3：2 D、2：3：2：3

    查看试题解析

  • 2. 如图，在等腰梯形ABCD中，AD∥BC，AD=5，AB=6，BC=8，且AB∥DE，则△DEC的周长是（  ）.

    A、3 B、12 C、15 D、19

    查看试题解析

  • 3. 四边形ABCD中，AB∥CD，要使ABCD是平行四边形，需要补充的一个条件（   ）
    A、AD=BC B、AB=CD C、∠DAB=∠ABC D、∠ABC=∠BCD

    查看试题解析

  • 4. 如图， ▱ABCD 中， EG//FH//CD ，则图中平行四边形有（   ）

    A、3个 B、4个 C、5个 D、6个

    查看试题解析

  • 5. 如图，在四边形ABCD中，已知AB∥CD，再添加一个条件 ， 则四边形ABCD是平行四边形(图中不再添加辅助线)

    查看试题解析

  • 6. 如图所示，在▱ABCD中，E，F分别为AB，DC的中点，连接DE，EF，FB，则图中共有个平行四边形．

    查看试题解析

  • 7. 若四边形ABCD的边AB＝CD，BC＝DA，则这个四边形是 ， 理由是 ．

    查看试题解析

  • 8. 如图，在▱ABCD中，E、F分别是BC、AD边上的点，且∠1=∠2.求证：四边形AECF是平行四边形.

    查看试题解析

  • 9. 如图所示 ▱ ABCD中，E，F分别是边AD，BC上的点，且AE=CF，

    (1)、求证：BE=DF
    (2)、连结AF，若AD=DF，∠ADF=40°，求∠AFB的度数。

    查看试题解析

  • 10. 如图，在 ▱ABCD 中， AE⊥BD 于 E ， CF⊥BD 于 F ，连接 AF ， CE .求证：四边形 AECF 是平行四边形.

    查看试题解析

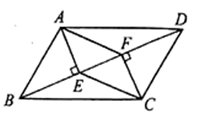
二、提高特训

  • 11. 如图， E 、 F 分别是平行四边形 ABCD 的边 AD 、 BC 上的点，且 BE//DF ， AC 分别交 BE 、 DF 于点 G 、 H .下列结论：①四边形 BFDE 是平行四边形；② ΔAGE≅ΔCHF ；③ BG=DH ；④ SΔAGE：SΔCDH=GE：DH ，其中正确的个数是（   ）

    A、1个 B、2个 C、3个 D、4个

    查看试题解析

  • 12. 若以A(-1，0)，B(3，0)，C(0，1)三点为顶点画平行四边形，则第四个顶点不可能在（ ）
    A、第一象限 B、第二象限 C、第三象限 D、第四象限

    查看试题解析

  • 13. 如图，P是∠ABC内一点，点Q在BC上，过点P画直线a∥BC，过点Q画直线b∥AB，若∠ABC=115°，则直线a与b相交所成的锐角的度数为(   ）

    A、25° B、45° C、65° D、85°

    查看试题解析

  • 14. 如图，在▱ABCD中，点E，F分别在边AB和CD上，下列条件不能判定四边形DEBF一定是平行四边形的是（ ）

    A、AE＝CF B、DE＝BF C、∠ADE＝∠CBF D、∠AED＝∠CFB

    查看试题解析

  • 15. 如图，△ABC中，AB＝AC＝6， BC=5 ，点M在BC上，ME∥AC，交AB于点E，MF∥AB，交AC于点F，则四边形MEAF的周长是

    查看试题解析

  • 16. 如图，在平行四边形ABCD中，点E、F在AC上，且AF＝CE，点G、H分别在AB、CD上，且AG＝CH，AC与GH相交于点O.

    (1)、求证：EG//FH；
    (2)、GH、EF互相平分.

    查看试题解析