浙江省杭州市萧山区2019-2020学年七年级上学期数学期末考试试卷
试卷更新日期:2020-03-20 类型:期末考试
一、选择题:本题有10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一个是符合题目要求的。
-
1. 美丽的萧山是一个充满生机和活力的地域,它古老而又年轻,区内耕地面积约为760000亩。则760000用科学记数法可表示为( )A、76x104 B、76x105 C、7.6x105 D、7.6x1062. 如图,小明用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能解释这一现象的数学知识是( )
 A、经过一点能画无数条直线 B、两点之间,线段最短 C、两点确定一条直线 D、连接两点间的线段的长度,叫做这两点的距离3. 下列计算正确的是 ( )A、 B、 C、 D、4. 有理数a,b在数轴上表示如图所示,则下列各式中正确的是( )
A、经过一点能画无数条直线 B、两点之间,线段最短 C、两点确定一条直线 D、连接两点间的线段的长度,叫做这两点的距离3. 下列计算正确的是 ( )A、 B、 C、 D、4. 有理数a,b在数轴上表示如图所示,则下列各式中正确的是( )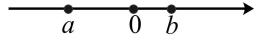 A、ab>0 B、|b|>|a| C、-a>b D、b<a5. 若代数式3a+1的值与3(a+1)的值互为相反数,则a的值为( )A、 B、 C、 D、6. 如图,点C,D在线段AB上.则下列表述或结论错误的是( )
A、ab>0 B、|b|>|a| C、-a>b D、b<a5. 若代数式3a+1的值与3(a+1)的值互为相反数,则a的值为( )A、 B、 C、 D、6. 如图,点C,D在线段AB上.则下列表述或结论错误的是( ) A、若AC=BD,则AD=BC B、AC=AD+DB-BC C、AD=AB+CD-BC D、图中共有线段12条7. 如图,以数轴的单位长度线段为边作一个正方形,以表示数1的点为圆心,正方形对角线长为半径画弧交数轴于点A,则点A表示的数是( )
A、若AC=BD,则AD=BC B、AC=AD+DB-BC C、AD=AB+CD-BC D、图中共有线段12条7. 如图,以数轴的单位长度线段为边作一个正方形,以表示数1的点为圆心,正方形对角线长为半径画弧交数轴于点A,则点A表示的数是( )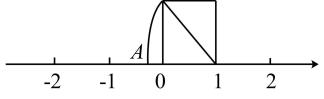 A、1- B、-1+ C、-1- D、-8. 下列计算正确的是( )A、6÷(-3-2)=-5 B、(- )÷(- )×3=1 C、-32× =-2 D、± =±0.129. 一套仪器由一个A部件和三个B部件构成,用1立方米钢板可做40个A部件或240个B部件。现要用6立方米钢板制作这种仪器,设应用x立方米钢板做B部件,其他钢板做A部件,恰好配套,则可列方程为( )A、3×40x=240(6-x) B、240x=3×40(6-x) C、40x=3×240(6-x) D、3×240x=40(6-x)10. 有一个不完整圆柱形玻璃密封容器如图①,测得其底面半径为a,高为h,其内装蓝色液体若干。若如图②放置时,测得液面高为 h;若如图③放置时,测得液面高为 h。则该玻璃密封容器的容积(圆柱体容积=底面积×高)是( )
A、1- B、-1+ C、-1- D、-8. 下列计算正确的是( )A、6÷(-3-2)=-5 B、(- )÷(- )×3=1 C、-32× =-2 D、± =±0.129. 一套仪器由一个A部件和三个B部件构成,用1立方米钢板可做40个A部件或240个B部件。现要用6立方米钢板制作这种仪器,设应用x立方米钢板做B部件,其他钢板做A部件,恰好配套,则可列方程为( )A、3×40x=240(6-x) B、240x=3×40(6-x) C、40x=3×240(6-x) D、3×240x=40(6-x)10. 有一个不完整圆柱形玻璃密封容器如图①,测得其底面半径为a,高为h,其内装蓝色液体若干。若如图②放置时,测得液面高为 h;若如图③放置时,测得液面高为 h。则该玻璃密封容器的容积(圆柱体容积=底面积×高)是( )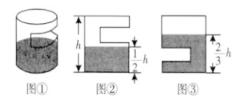 A、 a2h B、 a2h C、 a2h D、 ah
A、 a2h B、 a2h C、 a2h D、 ah二、填空题:本题有6小题,每小题3分,共18分。
-
11. 写出一个3次单项式。12. 已知x=3是方程ax=a+10的解,则a的值是 。13. 如图,直线AB,CD相交于点O,射线OE⊥CD, 给出下列结论:①∠2和∠4互为对顶角;②∠3+∠2=180°;③∠5与∠4互补;④∠5=∠3-∠1;其中正确的是。(填序号)
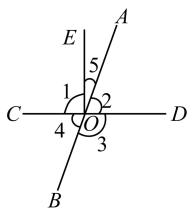 14. 已知a,b,c为互不相等的整数,且abc=-4,则a+b+c=。15. 小明设计了一个如下图所示的电脑运算程序:
14. 已知a,b,c为互不相等的整数,且abc=-4,则a+b+c=。15. 小明设计了一个如下图所示的电脑运算程序: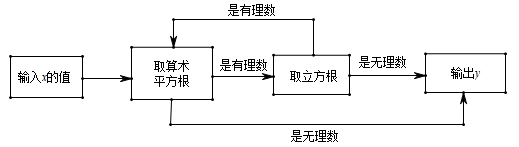 (1)、当输入x的值是64时,输出的y值是。(2)、分析发现,当实数x取 时,该程序无法输出y值。16. “格子乘法”作为两个数相乘的一种计算方法最早在15世纪由意大利数学家帕乔利提出,在明代的《算法统宗》一书中被称为“铺地锦”。如图1,计算47x51,将乘数47计入上行,乘数51计入右行,然后以乘数47的每位数字乘以乘数51的每位数字,将结果计入相应的格子中,最后按斜行加起来,得2397。
(1)、当输入x的值是64时,输出的y值是。(2)、分析发现,当实数x取 时,该程序无法输出y值。16. “格子乘法”作为两个数相乘的一种计算方法最早在15世纪由意大利数学家帕乔利提出,在明代的《算法统宗》一书中被称为“铺地锦”。如图1,计算47x51,将乘数47计入上行,乘数51计入右行,然后以乘数47的每位数字乘以乘数51的每位数字,将结果计入相应的格子中,最后按斜行加起来,得2397。 (1)、如图2,用“格子乘法”表示25×81,则m的值为。(2)、如图3,用“格子乘法”表示两个两位数相乘,则a的值为 。
(1)、如图2,用“格子乘法”表示25×81,则m的值为。(2)、如图3,用“格子乘法”表示两个两位数相乘,则a的值为 。三、解答题:本题有7小题,共52分.解答应写出文字说明或推演步骤。
-
17. 计算:(1)、5×(-2)-(-1)(2)、(-1)4-6÷(-3)18. 如图,已知平面内有A,B,C三个点,根据下列语句画出图形:
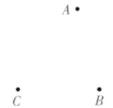
①画射线CB。
②连接AB,AC,用直尺和圆规在射线CB上取一点D,使CD=BC+AC-AB(不写作法,保留作图痕迹)。
19. 解方程:(1)、3(x-2)+6x=5(2)、20. 计算:(1)、(2)、21. 如图, 直线AB,CD相交于点O,已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3。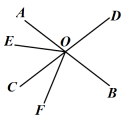 (1)、求∠AOE的度数;(2)、若OF平分∠BOE,试说明OB是∠DOF的平分线的理由。22.(1)、化简或计算下列两题:
(1)、求∠AOE的度数;(2)、若OF平分∠BOE,试说明OB是∠DOF的平分线的理由。22.(1)、化简或计算下列两题:①已知x2-5=2y,求-5(x2-2xy)+(2x2-10xy)+6y的值。
②已知x=2是关于x的一元一次方程(3a-1)x=2b+4的解,求6-3a+b的值。
(2)、写出上述①、②题共同体现的数学思想。23. 如图,在数轴上A点表示的数是-8,B点表示的数是2。动线段CD=4(点D在点C的右侧),从点C与点A重合的位置出发,以每秒2个单位的速度向右运动,运动时间为t秒。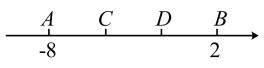 (1)、①已知点C表示的数是-6,试求点D表示的数;
(1)、①已知点C表示的数是-6,试求点D表示的数;②用含有t的代数式表示点D表示的数。
(2)、当AC=2BD时,求t的值。(3)、试问当线段CD在什么位置时,AD+BC或AD-BC的值始终保持不变?请求出它的值并说明此时线段CD的位置。