人教版数学九年级上册第25章 25.1.2概率 同步练习
试卷更新日期：2017-08-25 类型：同步测试
一、单选题
-
1. 在一个不透明的袋子中装有4个红球和3个黑球，它们除颜色外其它均相同，从中任意摸出一个球，则摸出黑球的概率是（ ）
A、 B、 C、 D、2. 从 ，0，π，3.14，6这5个数中随机抽取一个数，抽到有理数的概率是（ ）A、 B、 C、 D、3. 如图，共有12个大小相同的小正方形，其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分，现从其余的小正方形中任取一个涂上阴影，能构成这个正方体的表面展开图的概率是（ ）
A、 B、 C、 D、4. 从一副洗匀的普通扑克牌中随机抽取一张，则抽出红桃的概率是（ ）A、 B、 C、 D、5. 下列图形：
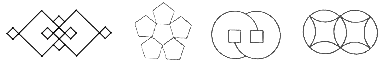
任取一个是中心对称图形的概率是（ ）
A、 B、 C、 D、16. 下列说法正确的是（ ）A、检测某批次灯泡的使用寿命，适宜用全面调查 B、可能性是1%的事件在一次试验中一定不会发生 C、数据3，5，4，1，﹣2的中位数是4 D、“367中有2人同月同日初生”为必然事件7. 小明向如图所示的正方形ABCD区域内投掷飞镖，点E是以AB为直径的半圆与对角线AC的交点．如果小明投掷飞镖一次，则飞镖落在阴影部分的概率为（ ）
A、 B、 C、 D、8. 下列说法正确的是（ ）A、“经过有交通信号的路口，遇到红灯，”是必然事件 B、已知某篮球运动员投篮投中的概率为0.6，则他投10次一定可投中6次 C、处于中间位置的数一定是中位数 D、方差越大数据的波动越大，方差越小数据的波动越小9. 在一个不透明的口袋里有红、黄、蓝三种颜色的小球，这些球除颜色外部相同，其中有5个黄球，4个蓝球．若随机摸出一个蓝球的概率为 ，则随机摸出一个红球的概率为（ ）A、 B、 C、 D、10. 某收费站在2小时内对经过该站的机动车统计如下：类型
轿车
货车
客车
其他
数量（辆）
36
24
8
12
若有一辆机动车将经过这个收费站，利用上面的统计估计它是轿车的概率为（ ）
A、 B、 C、 D、二、填空题
-
11. 不透明袋子中装有6个球，其中有5个红球、1个绿球，这些球除颜色外无其他差别．从袋子中随机取出1个球，则它是红球的概率是 ．12. 某同学家长应邀参加孩子就读中学的开放日活动，他打算上午随机听一节孩子所在1班的课，下表是他拿到的当天上午1班的课表，如果每一节课被听的机会均等，那么他听数学课的概率是 ．
班级
节次
1班
第1节
语文
第2节
英语
第3节
数学
第4节
音乐
13. 如图所示的圆形纸板被等分成10个扇形挂在墙上，玩飞镖游戏（每次飞镖均落在纸板上），则飞镖落在阴影区域的概率是 ．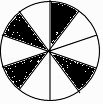
14. 不透明的布袋里有2个黄球、3个红球、5个白球，它们除颜色外其它都相同，那么从布袋中任意摸出一球恰好为红球的概率是 ．15. 一个不透明的盒子里有5张完全相同的卡片，它们的标号分别为1，2，3，4，5，随机抽取一张，抽中标号为奇数的卡片的概率是 ．16. 在一个不透明的袋子中装有除颜色外完全相同的3个红球、3个黄球、2个绿球，任意摸出一球，摸到红球的概率是 ．17. 从“线段，等边三角形，圆，矩形，正六边形”这五个圆形中任取一个，取到既是轴对称图形又是中心对称图形的概率是 ．18. 一个箱子装有除颜色外都相同的2个白球，2个黄球，1个红球．现添加同种型号的1个球，使得从中随机抽取1个球，这三种颜色的球被抽到的概率都是 ，那么添加的球是 ．19. 毛泽东在《沁园春•雪》中提到五位历史名人：秦始皇、汉武帝、唐太宗、宋太祖、成吉思汗，小红将这五位名人简介分别写在五张完全相同的知识卡片上，小哲从中随机抽取一张，卡片上介绍的人物是唐朝以后出生的概率是 ．三、综合题
-
20. 全面两孩政策实施后，甲、乙两个家庭有了各自的规划，假定生男生女的概率相同，回答下列问题：(1)、甲家庭已有一个男孩，准备再生一个孩子，则第二个孩子是女孩的概率是；(2)、乙家庭没有孩子，准备生两个孩子，求至少有一个孩子是女孩的概率．21. 为落实“垃圾分类”，环卫部门要求垃圾要按A，B，C三类分别装袋，投放，其中A类指废电池，过期药品等有毒垃圾，B类指剩余食品等厨余垃圾，C类指塑料，废纸等可回收垃圾．甲投放了一袋垃圾，乙投放了两袋垃圾，这两袋垃圾不同类．(1)、直接写出甲投放的垃圾恰好是A类的概率；(2)、求乙投放的垃圾恰有一袋与甲投放的垃圾是同类的概率．22. 由于只有1张市运动会开幕式的门票，小王和小张都想去，两人商量采取转转盘（如图，转盘盘面被分为面积相等，且标有数字1，2，3，4的4个扇形区域）的游戏方式决定谁胜谁去观看．规则如下：两人各转动转盘一次，当转盘指针停止，如两次指针对应盘面数字都是奇数，则小王胜；如两次指针对应盘面数字都是偶数，则小张胜；如两次指针对应盘面数字是一奇一偶，视为平局．若为平局，继续上述游戏，直至分出胜负．
如果小王和小张按上述规则各转动转盘一次，则
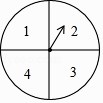(1)、小王转动转盘，当转盘指针停止，对应盘面数字为奇数的概率是多少？(2)、该游戏是否公平？请用列表或画树状图的方法说明理由．23. 车辆经过润扬大桥收费站时，4个收费通道 A、B、C、D中，可随机选择其中的一个通过．(1)、一辆车经过此收费站时，选择 A通道通过的概率是；(2)、求两辆车经过此收费站时，选择不同通道通过的概率．24.如图，有四张背面完全相同的纸牌A、B、C、D，其正面分别画有四个不同的几何图形，将这四张纸牌背面朝上洗匀．
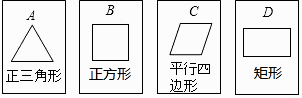(1)、从中随机摸出一张，求摸出的牌面图形是中心对称图形的概率；(2)、小明和小亮约定做一个游戏，其规则为：先由小明随机摸出一张纸牌，不放回，再由小亮从剩下的纸牌中随机摸出一张，若摸出的两张牌面图形都是轴对称图形小明获胜，否则小亮获胜，这个游戏公平吗？请用列表法（或树状图）说明理由（纸牌用A、B、C、D表示）．