河南省郑州市2020年数学中考模拟试卷

试卷更新日期：2020-03-20 类型：中考模拟

进入出卷网下载

一、选择题（本大题共12小题，每小题3分，共36分）

1. 如果a的倒数是﹣1，则a²⁰¹⁹的值是（）

A、1 B、﹣1 C、2019 D、﹣2019

查看试题解析
2. 2019年11日凌晨，阿里巴巴公布了2019双十一购物狂欢节的相关数据：33分53秒时，成交额破200亿.200亿用科学记数法表示为（）

A、 0.2×10¹⁰ B、2×10¹⁰ C、2×10⁹ D、20×10⁹

查看试题解析
3. 既是轴对称图形，又是中心对称图形的是（）

A、等边三角形 B、等腰梯形 C、平行四边形 D、正六边形

查看试题解析
4. 在某校“我的中国梦”演讲比赛中，有7名学生参加决赛，他们决赛的最终成绩各不相同，其中一名学生想要知道自己能否进入前3名，他不仅要了解自己的成绩，还要了解这7名学生成绩的（）

A、众数 B、方差 C、平均数 D、中位数

查看试题解析
5. 下列等式错误的是（）

A、（2mn）²=4m²n² B、（﹣2mn）²=4m²n² C、（2m²n²）³=8m⁶n⁶ D、（﹣2m²n²）³=﹣8m⁵n⁵

查看试题解析
6. 互联网“微商”经营已成为大众创业新途径，某微信平台上一件商品标价为200元，按标价的五折销售，仍可获利20元，则这件商品的进价为（　　）

A、120元 B、100元 C、80元 D、60元

查看试题解析
7. 如图，直线y=﹣x+2与y=ax+b（a≠0且a，b为常数）的交点坐标为（3，﹣1），则关于x的不等式﹣x+2≥ax+b的解集为（　　）

A、x≥﹣1 B、x≥3 C、x≤﹣1 D、x≤3

查看试题解析
8. 如图，在三角形ABC中，∠ACB=90°，∠B=50°，将此三角形绕点C沿顺时针方向旋转后得到三角形A′B′C，若点B′恰好落在线段AB上，AC、A′B′交于点O，则∠COA′的度数是（）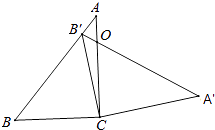

A、50° B、60° C、70° D、80°

查看试题解析
9. A，B两地相距180km，新修的高速公路开通后，在A，B两地间行驶的长途客车平均车速提高了50%，而从A地到B地的时间缩短了1h．若设原来的平均车速为xkm/h，则根据题意可列方程为（）

A、 $\frac{180}{x}$ ﹣ $\frac{180}{(1 + 50 %) x}$ =1 B、 $\frac{180}{(1 + 50 %) x}$ ﹣ $\frac{180}{x}$ =1 C、 $\frac{180}{x}$ ﹣ $\frac{180}{(1 - 50 %) x}$ =1 D、 $\frac{180}{(1 - 50 %) x}$ ﹣ $\frac{180}{x}$ =1

查看试题解析
10. 如图是抛物线y₁=ax²+bx+c（a≠0）图象的一部分，抛物线的顶点坐标A（1，3），与x轴的一个交点B（4，0），直线y₂=mx+n（m≠0）与抛物线交于A，B两点，下列结论：
①2a+b=0；②abc＞0；③方程ax²+bx+c=3有两个相等的实数根；④抛物线与x轴的另一个交点是（﹣1，0）；⑤当1＜x＜4时，有y₂＜y₁ ，
其中正确的是（　　）

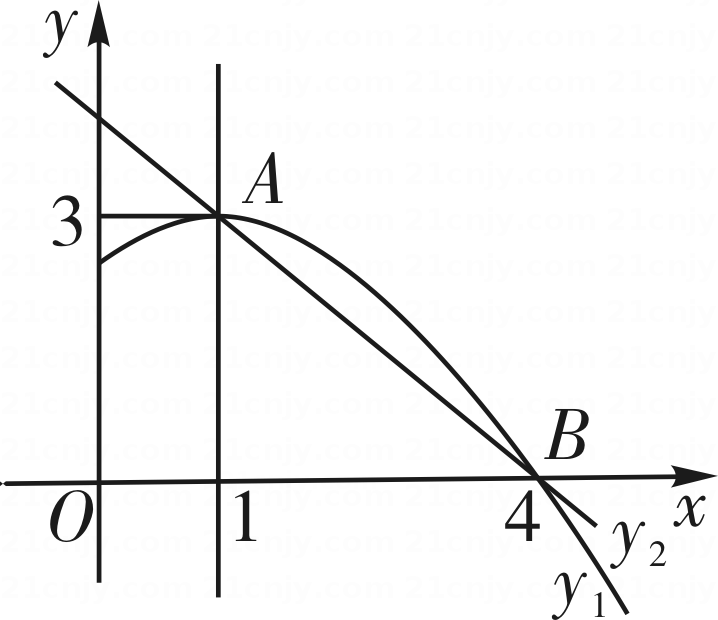A、①②③ B、①③④ C、①③⑤ D、②④⑤

查看试题解析
11. 在等腰直角三角形ABC中，AB=AC=4，点O为BC的中点，以O为圆心作⊙O交BC于点M、N，⊙O与AB、AC相切，切点分别为D、E，则⊙O的半径和∠MND的度数分别为（）

A、2，22.5° B、3，30° C、3，22.5° D、2，30°

查看试题解析
12.
如图，在正方形ABCD中，AC为对角线，E为AB上一点，过点E作EF∥AD，与AC、DC分别交于点G，F，H为CG的中点，连接DE，EH，DH，FH．下列结论：
①EG=DF；②∠AEH+∠ADH=180°；③△EHF≌△DHC；④若 $\frac{A E}{A B} = \frac{2}{3}$ ，则3S_△_EDH=13S_△_DHC ，其中结论正确的有（）

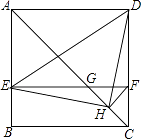A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（每题3分，共12分）

13. 分解因式：（m+1）（m﹣9）+8m= ．

查看试题解析
14. 如图所示的电路图中，在开关全部断开的情况下，闭合其中任意一个开关，灯泡发亮的概率是．

查看试题解析
15. 兴趣小组的同学要测量树的高度．在阳光下，一名同学测得一根长为1米的竹竿的影长为0.4米，同时另一名同学测量树的高度时，发现树的影子不全落在地面上，有一部分落在教学楼的第一级台阶上，测得此影子长为0.2米，一级台阶高为0.3米，如图所示，若此时落在地面上的影长为4.4米，则树高为．

查看试题解析
16. 如图，△AOB为等边三角形，点B的坐标为（﹣2，0），过点C（2，0）作直线l交AO于D，交AB于E，点E在某反比例函数图象上，当△ADE和△DCO的面积相等时，那么该反比例函数解析式为．

查看试题解析

三、解答题（本大题共8题，共52分）

17. 计算. ${(- 2011)}^{0} + {(\frac{\sqrt{2}}{2})}^{- 1} + | \sqrt{2} - 2 | - 2 \cos 0^{\circ}$

查看试题解析
18. 先化简，再求值： $(1 - \frac{1}{x + 2}) \div \frac{x^{2} + 2 x + 1}{x^{2} - 4}$ ，其中 $x = \sqrt{2} - 1$ ．

查看试题解析
19. 某学校九年级学生举行朗诵比赛，全年级学生都参加，学校对表现优异的学生进行表彰，设置一、二、三等奖各进步奖共四个奖项，赛后将九年级（1）班的获奖情况绘制成如图所示的两幅不完整的统计图，请根据图中的信息，解答下列问题：

(1)、九年级（1）班共有名学生；

(2)、将条形图补充完整：在扇形统计图中，“二等奖”对应的扇形的圆心角度数是；

(3)、如果该九年级共有1250名学生，请估计荣获一、二、三等奖的学生共有多少名．

查看试题解析
20. 如图，在菱形ABCD中，对角线AC与BD相交于点O，MN过点O且与边AD、BC分别交于点M和点N．

(1)、请你判断OM和ON的数量关系，并说明理由；

(2)、过点D作DE∥AC交BC的延长线于点E，当AB=6，AC=8时，求△BDE的周长

查看试题解析
21. 某大型企业为了保护环境，准备购买A、B两种型号的污水处理设备共8台，用于同时治理不同成分的污水，若购买A型2台、B型3台需54万，购买A型4台、B型2台需68万元．

(1)、求出A型、B型污水处理设备的单价；

(2)、经核实，一台A型设备一个月可处理污水220吨，一台B型设备一个月可处理污水190吨，如果该企业每月的污水处理量不低于1565吨，请你为该企业设计一种最省钱的购买方案．

查看试题解析
22. 如图，在Rt△ABC中，∠C=90°，点O在AB上，经过点A的⊙O与BC相切于点D，与AC，AB分别相交于点E，F，连接AD与EF相交于点G．

(1)、求证：AD平分∠CAB；

(2)、若OH⊥AD于点H，FH平分∠AFE，DG=1．
①试判断DF与DH的数量关系，并说明理由；

②求⊙O的半径．

查看试题解析
23. 如图，已知一条直线过点（0，4），且与抛物线y= $\frac{1}{4}$ x²交于A，B两点，其中点A的横坐标是﹣2．

(1)、求这条直线的函数关系式及点B的坐标．

(2)、在x轴上是否存在点C，使得△ABC是直角三角形？若存在，求出点C的坐标，若不存在，请说明理由．

(3)、过线段AB上一点P，作PM∥x轴，交抛物线于点M，点M在第一象限，点N（0，1），当点M的横坐标为何值时，MN+3MP的长度最大？最大值是多少？

查看试题解析