人教版数学九年级上册第24章 24.4弧长及扇形的面积 同步练习
试卷更新日期:2017-08-25 类型:同步测试
一、单选题
-
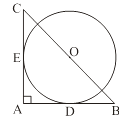
1. 如图,在Rt△ABC中,∠A=90°,BC= .以BC的中点O为圆心的圆分别与AB、AC相切于D、E两点,则 的长为 ( )
 A、 B、 C、 D、2.
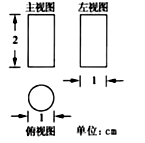
A、 B、 C、 D、2.如图是按 的比例画出的一个几何体的三视图,则该几何体的侧面积是( )
 A、 B、 C、 D、3. 如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是( )
A、 B、 C、 D、3. 如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是( )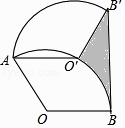 A、 B、2 ﹣ C、2 ﹣ D、4 ﹣4. 如图,在半径为4的⊙O中,CD是直径,AB是弦,且CD⊥AB,垂足为点E,∠AOB=90°,则阴影部分的面积是( )
A、 B、2 ﹣ C、2 ﹣ D、4 ﹣4. 如图,在半径为4的⊙O中,CD是直径,AB是弦,且CD⊥AB,垂足为点E,∠AOB=90°,则阴影部分的面积是( )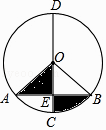 A、4π﹣4 B、2π﹣4 C、4π D、2π5. 圆锥的底面半径r=3,高h=4,则圆锥的侧面积是( )
A、4π﹣4 B、2π﹣4 C、4π D、2π5. 圆锥的底面半径r=3,高h=4,则圆锥的侧面积是( )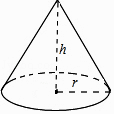 A、12π B、15π C、24π D、30π6. 若圆锥的侧面积等于其底面积的3倍,则该圆锥侧面展开图所对应扇形圆心角的度数为( )A、60° B、90° C、120° D、180°7. 如图,将矩形ABCD绕其右下角的顶点按顺时针方向旋转90°至图①位置,继续绕右下角的顶点按顺时针方向旋转90°至图②位置,以此类推,这样连续旋转2017次.若AB=4,AD=3,则顶点A在整个旋转过程中所经过的路径总长为( )
A、12π B、15π C、24π D、30π6. 若圆锥的侧面积等于其底面积的3倍,则该圆锥侧面展开图所对应扇形圆心角的度数为( )A、60° B、90° C、120° D、180°7. 如图,将矩形ABCD绕其右下角的顶点按顺时针方向旋转90°至图①位置,继续绕右下角的顶点按顺时针方向旋转90°至图②位置,以此类推,这样连续旋转2017次.若AB=4,AD=3,则顶点A在整个旋转过程中所经过的路径总长为( )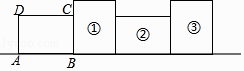 A、2017π B、2034π C、3024π D、3026π8. 如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1.把△ABC分别绕直线AB和BC旋转一周,所得几何体的地面圆的周长分别记作l1 , l2 , 侧面积分别记作S1 , S2 , 则( )
A、2017π B、2034π C、3024π D、3026π8. 如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1.把△ABC分别绕直线AB和BC旋转一周,所得几何体的地面圆的周长分别记作l1 , l2 , 侧面积分别记作S1 , S2 , 则( )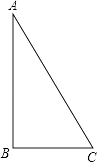 A、l1:l2=1:2,S1:S2=1:2 B、l1:l2=1:4,S1:S2=1:2 C、l1:l2=1:2,S1:S2=1:4 D、l1:l2=1:4,S1:S2=1:49. 如图,是一个几何体的三视图,根据图中所示数据计算这个几何体的侧面积是( )
A、l1:l2=1:2,S1:S2=1:2 B、l1:l2=1:4,S1:S2=1:2 C、l1:l2=1:2,S1:S2=1:4 D、l1:l2=1:4,S1:S2=1:49. 如图,是一个几何体的三视图,根据图中所示数据计算这个几何体的侧面积是( )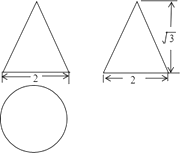 A、π B、2π C、4π D、5π10. 如图,已知扇形OAB的圆心角为60°,扇形的面积为6π,则该扇形的弧长为 .
A、π B、2π C、4π D、5π10. 如图,已知扇形OAB的圆心角为60°,扇形的面积为6π,则该扇形的弧长为 .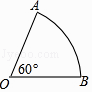
二、填空题
-
11. 圆锥底面半径为3cm,母线长3 cm则圆锥的侧面积为
cm2 .
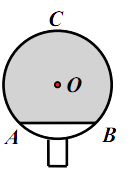
12.如图,小明自制一块乒乓球拍,正面是半径为 的 , ,弓形 (阴影部分)粘贴胶皮,则胶皮面积为 .
 13. 如图,扇形纸扇完全打开后,外侧两竹条AB,AC的夹角为120°,AB长为30cm,则
13. 如图,扇形纸扇完全打开后,外侧两竹条AB,AC的夹角为120°,AB长为30cm,则弧BC的长为cm(结果保留 )
 14. 圆锥的底面半径长为5,将其侧面展开后得到一个半圆,则该半圆的半径长是 .15. 如图,点O是线段AB上一点,AB=4cm,AO=1cm,若线段AB绕点O顺时针旋转120°到线段A′B′的位置,则线段AB在旋转过程中扫过的图形的面积为
14. 圆锥的底面半径长为5,将其侧面展开后得到一个半圆,则该半圆的半径长是 .15. 如图,点O是线段AB上一点,AB=4cm,AO=1cm,若线段AB绕点O顺时针旋转120°到线段A′B′的位置,则线段AB在旋转过程中扫过的图形的面积为cm2 . (结果保留π)
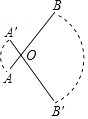 16. 如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=2 ,则图中阴影部分面积是(结果保留π和根号)
16. 如图,四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OA、OB、OC、AC,OB与AC相交于点E,若∠COB=3∠AOB,OC=2 ,则图中阴影部分面积是(结果保留π和根号)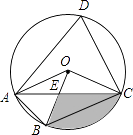 17. 如图,在△ABC中,∠ACB=90°,∠ABC=60°,AB=12cm,将△ABC以点B为中心顺时针旋转,使点C旋转到AB边延长线上的点D处,则AC边扫过的图形(阴影部分)的面积是cm2 . (结果保留π).
17. 如图,在△ABC中,∠ACB=90°,∠ABC=60°,AB=12cm,将△ABC以点B为中心顺时针旋转,使点C旋转到AB边延长线上的点D处,则AC边扫过的图形(阴影部分)的面积是cm2 . (结果保留π). 18. 如图,在圆心角为90°的扇形OAB中,半径OA=4,C为 的中点,D、E分别为OA,OB的中点,则图中阴影部分的面积为 .
18. 如图,在圆心角为90°的扇形OAB中,半径OA=4,C为 的中点,D、E分别为OA,OB的中点,则图中阴影部分的面积为 .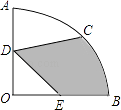 19. 已知:如同,△ABC内接于⊙O,且半径OC⊥AB,点D在半径OB的延长线上,且∠A=∠BCD=30°,AC=2,则由 ,线段CD和线段BD所围成图形的阴影部分的面积为 .
19. 已知:如同,△ABC内接于⊙O,且半径OC⊥AB,点D在半径OB的延长线上,且∠A=∠BCD=30°,AC=2,则由 ,线段CD和线段BD所围成图形的阴影部分的面积为 . 20. 如图,将矩形ABCD绕点C沿顺时针方向旋转90°到矩形A′B′CD′的位置,AB=2,AD=4,则阴影部分的面积为 .
20. 如图,将矩形ABCD绕点C沿顺时针方向旋转90°到矩形A′B′CD′的位置,AB=2,AD=4,则阴影部分的面积为 .
三、解答题
-
21.
如图, 为 的直角边 上一点,以 为半径的 与斜边 相切于点 ,交 于点 .已知 , .
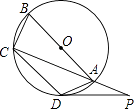
 (1)、求 的长;(2)、求图中阴影部分的面积.22. 如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点P在CA的延长线上,∠CAD=45°.
(1)、求 的长;(2)、求图中阴影部分的面积.22. 如图,四边形ABCD内接于⊙O,AB是⊙O的直径,点P在CA的延长线上,∠CAD=45°.(Ⅰ)若AB=4,求 的长;
(Ⅱ)若 = ,AD=AP,求证:PD是⊙O的切线.
 23. 如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
23. 如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.(Ⅰ)试判断直线BC与⊙O的位置关系,并说明理由;
(Ⅱ)若BD=2 ,BF=2,求阴影部分的面积(结果保留π).

四、综合题
-
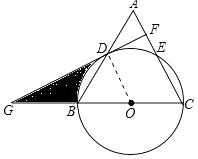
24. 在等腰△ABC中,AC=BC,以BC为直径的⊙O分别与AB,AC相交于点D,E,过点D作DF⊥AC,垂足为点F.
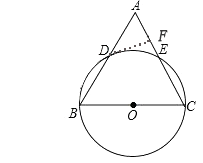 (1)、求证:DF是⊙O的切线;(2)、分别延长CB,FD,相交于点G,∠A=60°,⊙O的半径为6,求阴影部分的面积.
(1)、求证:DF是⊙O的切线;(2)、分别延长CB,FD,相交于点G,∠A=60°,⊙O的半径为6,求阴影部分的面积.