人教版数学九年级上册第24章 24.3正多边形和圆 同步练习
试卷更新日期：2017-08-25 类型：同步测试
一、单选题
-
1. 若正方形的外接圆半径为2，则其内切圆半径为（ ）A、 B、2 C、 D、12. 如图，正五边形ABCDE内接于⊙O，若⊙O的半径为5，则 的长度为（ ）
A、π B、2π C、5π D、10π3. 如图，将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心，AB为半径的扇形（忽略铁丝的粗细）．则所得扇形AFB（阴影部分）的面积为（ ）
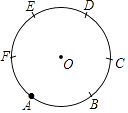
A、6π B、18 C、18π D、204. 如图，把正六边形各边按同一方向延长，使延长的线段与原正六边形的边长相等，顺次连接这六条线段外端点可以得到一个新的正六边形，…，重复上述过程，经过2018次后，所得到的正六边形边长是原正六边形边长的（ ）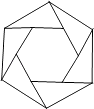
A、（ ）2016倍 B、（ ）2017倍 C、（ ）2018倍 D、（ ）2019倍5. 尺规作图特有的魅力曾使无数人沉湎其中，连当年叱咤风云的拿破仑也不例外，我们可以只用圆规将圆等分．例如可将圆6等分，如图只需在⊙O上任取点A，从点A开始，以⊙O的半径为半径，在⊙O上依次截取点B，C，D，E，F．从而点A，B，C，D，E，F把⊙O六等分．下列可以只用圆规等分的是（ ）①两等分 ②三等分 ③四等分 ④五等分．
A、② B、①② C、①②③ D、①②③④6. 如图，正方形ABCD内接于半径为2的⊙O，则图中阴影部分的面积为（ ）
A、π+1 B、π+2 C、π﹣1 D、π﹣27. 下列说法正确的是（ ）A、圆内接正六边形的边长与该圆的半径相等 B、在平面直角坐标系中，不同的坐标可以表示同一点 C、一元二次方程ax2+bx+c=0（a≠0）一定有实数根 D、将△ABC绕A点按顺时针方向旋转60°得△ADE，则△ABC与△ADE不全等8. 下列圆的内接正多边形中，一条边所对的圆心角最大的图形是（ ）A、正三角形 B、正方形 C、正五边形 D、正六边形9. 正多边形的中心角与该正多边形一个内角的关系是（ ）A、互余 B、互补 C、互余或互补 D、不能确定10. 如图，由7个形状、大小完全相同的正六边形组成的网格，正六边形的顶点称为格点，已知每个正六边形的边长为1，△ABC的顶点都在格点上，则△ABC的面积是（ ）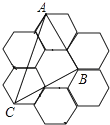
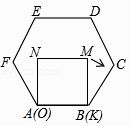
A、 B、2 C、3 D、311. 如图，已知五边形ABCDE 是⊙O 的内接正五边形，且⊙O 的半径为1．则图中阴影部分的面积是（ ）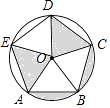
A、 B、 C、 D、12. 已知正方形MNOK和正六边形ABCDEF边长均为1，把正方形放在正六边形中，使OK边与AB边重合，如图所示，按下列步骤操作：将正方形在正六边形中绕点B顺时针旋转，使KM边与BC边重合，完成第一次旋转；再绕点C顺时针旋转，使MN边与CD边重合，完成第二次旋转；…在这样连续6次旋转的过程中，点B，M间的距离可能是（ ）
A、1.4 B、1.1 C、0.8 D、0.5二、填空题
-
13.
如图，有一个不定的正方形ABCD，它的两个相对的顶点A，C分别在边长为1的正六边形一组对边上，另外两个顶点B，D在正六边形内部（包括边界），则正方形边长a的取值范围是
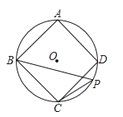
14. 如图，正六边形A1B1C1D1E1F1的边长为1，它的六条对角线又围成一个正六边形A2B2C2D2E2F2 ， 如此继续下去，则正六边形A4B4C4D4E4F4的面积是.
15. 正六边形的边长为8cm，则它的面积为cm2 ．16. 如图，⊙O的内接正五边形ABCDE的对角线AD与BE相交于点G，AE=2，则EG的长是 ．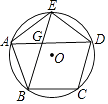
17. 正八边形的中心角等于度．18. 如图，AB为⊙O的内接正多边形的一边，已知∠OAB=70°，则这个正多边形的内角和为 ．
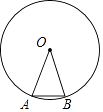19. 我们规定：一个正n边形（n为整数，n≥4）的最短对角线与最长对角线长度的比值叫做这个正n边形的“特征值”，记为λn ， 那么λ6= ．20. 半径为2的圆内接正三角形，正四边形，正六边形的边心距之比为 ．21. 如图，在边长为2的正八边形中，把其不相邻的四条边均向两边延长相交成一个四边形ABCD，则四边形ABCD的周长是 ．
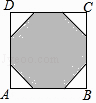22. 如图，正六边形ABCDEF内接于半径为3的圆O，则劣弧AB的长度为 ．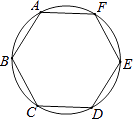
三、解答题
-
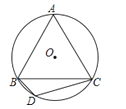
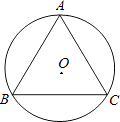
23. 如图，正三角形ABC内接于⊙O，若AB= cm，求⊙O的半径．
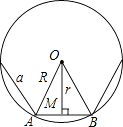
24. 如图，已知正n边形边长为a，边心距为r，求正n边形的半径R、周长P和面积S．
