人教版数学九年级上册第24章 24.2.2直线和圆的位置关系 同步练习
试卷更新日期:2017-08-25 类型:同步测试
一、综合题
-
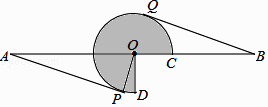
1. 如图,AB为⊙O的直径,CB,CD分别切⊙O于点B,D,CD交BA的延长线于点E,CO的延长线交⊙O于点G,EF⊥OG于点F.
 (1)、求证:∠FEB=∠ECF;(2)、若BC=6,DE=4,求EF的长.2. 如图,AB是⊙O直径,点C在⊙O上,AD平分∠CAB,BD是⊙O的切线,AD与BC相交于点E.
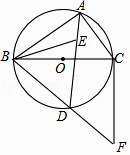
(1)、求证:∠FEB=∠ECF;(2)、若BC=6,DE=4,求EF的长.2. 如图,AB是⊙O直径,点C在⊙O上,AD平分∠CAB,BD是⊙O的切线,AD与BC相交于点E.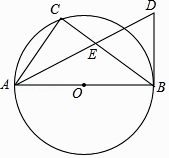 (1)、求证:BD=BE;(2)、若DE=2,BD= ,求CE的长.3. 如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.
(1)、求证:BD=BE;(2)、若DE=2,BD= ,求CE的长.3. 如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E. (1)、求证:AD平分∠BAC;(2)、若CD=1,求图中阴影部分的面积(结果保留π).4. 如图,已知AB是⊙O的直径,CD与⊙O相切于C,BE∥CO.
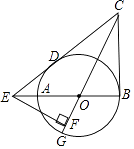
(1)、求证:AD平分∠BAC;(2)、若CD=1,求图中阴影部分的面积(结果保留π).4. 如图,已知AB是⊙O的直径,CD与⊙O相切于C,BE∥CO. (1)、求证:BC是∠ABE的平分线;(2)、若DC=8,⊙O的半径OA=6,求CE的长.5. 如图,已知平行四边形OABC的三个顶点A、B、C在以O为圆心的半圆上,过点C作CD⊥AB,分别交AB、AO的延长线于点D、E,AE交半圆O于点F,连接CF.
(1)、求证:BC是∠ABE的平分线;(2)、若DC=8,⊙O的半径OA=6,求CE的长.5. 如图,已知平行四边形OABC的三个顶点A、B、C在以O为圆心的半圆上,过点C作CD⊥AB,分别交AB、AO的延长线于点D、E,AE交半圆O于点F,连接CF. (1)、判断直线DE与半圆O的位置关系,并说明理由;(2)、①求证:CF=OC;
(1)、判断直线DE与半圆O的位置关系,并说明理由;(2)、①求证:CF=OC;②若半圆O的半径为12,求阴影部分的周长.
6. 如图,点A是直线AM与⊙O的交点,点B在⊙O上,BD⊥AM垂足为D,BD与⊙O交于点C,OC平分∠AOB,∠B=60°.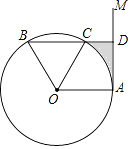 (1)、求证:AM是⊙O的切线;(2)、若DC=2,求图中阴影部分的面积(结果保留π和根号).7. 如图,AB为⊙O的直径,D为 的中点,连接OD交弦AC于点F,过点D作DE∥AC,交BA的延长线于点E.
(1)、求证:AM是⊙O的切线;(2)、若DC=2,求图中阴影部分的面积(结果保留π和根号).7. 如图,AB为⊙O的直径,D为 的中点,连接OD交弦AC于点F,过点D作DE∥AC,交BA的延长线于点E. (1)、求证:DE是⊙O的切线;(2)、连接CD,若OA=AE=4,求四边形ACDE的面积.8. 如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于D.
(1)、求证:DE是⊙O的切线;(2)、连接CD,若OA=AE=4,求四边形ACDE的面积.8. 如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于D.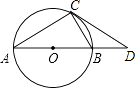 (1)、求证:△ADC∽△CDB;(2)、若AC=2,AB= CD,求⊙O半径.9. 如图,AB为⊙O的直径,点C在⊙O上,点P是直径AB上的一点(不与A重合),过点P作AB的垂线交BC于点Q.
(1)、求证:△ADC∽△CDB;(2)、若AC=2,AB= CD,求⊙O半径.9. 如图,AB为⊙O的直径,点C在⊙O上,点P是直径AB上的一点(不与A重合),过点P作AB的垂线交BC于点Q.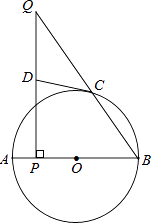 (1)、在线段PQ上取一点D,使DQ=DC,连接DC,试判断CD与⊙O的位置关系,并说明理由.(2)、若cosB= ,BP=6,AP=1,求QC的长.10. 在等腰△ABC中,AC=BC,以BC为直径的⊙O分别与AB,AC相交于点D,E,过点D作DF⊥AC,垂足为点F.
(1)、在线段PQ上取一点D,使DQ=DC,连接DC,试判断CD与⊙O的位置关系,并说明理由.(2)、若cosB= ,BP=6,AP=1,求QC的长.10. 在等腰△ABC中,AC=BC,以BC为直径的⊙O分别与AB,AC相交于点D,E,过点D作DF⊥AC,垂足为点F.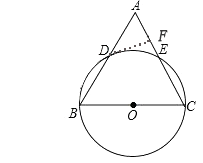 (1)、求证:DF是⊙O的切线;(2)、分别延长CB,FD,相交于点G,∠A=60°,⊙O的半径为6,求阴影部分的面积.
(1)、求证:DF是⊙O的切线;(2)、分别延长CB,FD,相交于点G,∠A=60°,⊙O的半径为6,求阴影部分的面积.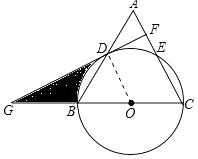 11. 已知:如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,过点D作DE⊥AD交AB于点E,以AE为直径作⊙O.
11. 已知:如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,过点D作DE⊥AD交AB于点E,以AE为直径作⊙O.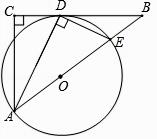 (1)、求证:BC是⊙O的切线;(2)、若AC=3,BC=4,求BE的长.
(1)、求证:BC是⊙O的切线;(2)、若AC=3,BC=4,求BE的长.