人教版数学九年级上册第24章 24.2.1点和圆的位置关系 同步练习
试卷更新日期：2017-08-25 类型：同步测试
一、单选题
-
1. 已知⊙O是△ABC的外接圆，边BC=4cm，且⊙O半径也为4cm，则∠A的度数是（ ）A、30° B、60°或120° C、150° D、30°或150°2. 如图，⊙O是△ABC的外接圆，直径AD与BC相交于点E，连接CD，若⊙O的半径为5，AB=AC=8，则EC长为（ ）
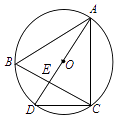A、4 B、 C、 D、3. 已知△ABC在正方形网格中的位置如图所示，则点P是△ABC的（ ）
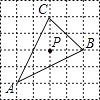A、外心 B、内心 C、三条高线的交点 D、三条中线的交点4. 如图，在矩形ABCD中，AB=4，BC=6，E是矩形内部的一个动点，且AE⊥BE，则线段CE的最小值为（ ）
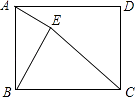A、 B、2 ﹣2 C、2 ﹣2 D、45. 如图，D是等边△ABC外接圆上的点，且∠DAC=20°，则∠ACD的度数为（ ）
A、20° B、30° C、40° D、45°6. 如图，锐角△ABC内接于⊙O，点D在⊙O外（与点C在AB同侧），∠ABD=90°，下列结论：①sinC＞sinD；②cosC＞cosD；③tanC＞tanD，正确的结论为（ ）
A、①② B、②③ C、①②③ D、①③7. 如图，Rt△ABC中，AB⊥BC，AB=6，BC=4，P是△ABC内部的一个动点，且满足∠PAB=∠PBC，则线段CP长的最小值为（ ）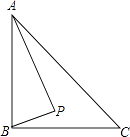
A、 B、2 C、 D、8. 如图，△ABC内接于⊙O，AC是⊙O的直径，∠ACB=40°，点D是弧BAC上一点，连结CD．则∠D的度数是（ ）
A、50° B、45° C、40° D、35°9. 如图，在平面直角坐标系xOy中，点A为（0，3），点B为（2，1），点C为（2，﹣3）．则经画图操作可知：△ABC的外心坐标应是（ ）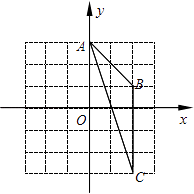
A、（0，0） B、（1，0） C、（﹣2，﹣1） D、（2，0）10. 公元前5世纪，毕达哥拉斯学派中的一名成员希伯索斯发现了无理数 ，导致了第一次数学危机， 是无理数的证明如下：假设 是有理数，那么它可以表示成 （p与q是互质的两个正整数）．于是（ ）2=（ ）2=2，所以，q2=2p2 ． 于是q2是偶数，进而q是偶数，从而可设q=2m，所以（2m）2=2p2 ， p2=2m2 ， 于是可得p也是偶数．这与“p与q是互质的两个正整数”矛盾．从而可知“ 是有理数”的假设不成立，所以， 是无理数．
这种证明“ 是无理数”的方法是（ ）
A、综合法 B、反证法 C、举反例法 D、数学归纳法二、填空题
-
11. 已知△ABC的外心为O，内心为I，∠BOC=120°，∠BIC= ．12. 若点O是等腰△ABC的外心，且∠BOC=60°，底边BC=2，则△ABC的面积为 ．13. 如图，点P是正方形ABCD的对角线BD上的一个动点（不与B、D重合），连结AP，过点B作直线AP的垂线，垂足为H，连结DH．若正方形的边长为4，则线段DH长度的最小值是 ．
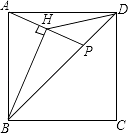14. 如图，AD是△ABC的高，AE是△ABC的外接圆⊙O的直径，且AB=6，AC=5，AD=3，则⊙O的直径AE= ．
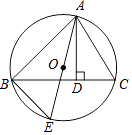15. 在Rt△ABC中，∠ACB=90°，AC=8，BC=6，点D是以点A为圆心4为半径的圆上一点，连接BD，点M为BD中点，线段CM长度的最大值为 ．
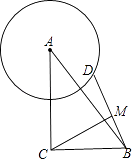16. 如图，△ABC是定圆O的内接三角形，AD为△ABC的高线，AE平分∠BAC交⊙O于E，交BC于G，连OE交BC于F，连OA，在下列结论中，①CE=2EF，②△ABG∽△AEC，③∠BAO=∠DAC，④ 为常量．其中正确的有 ．
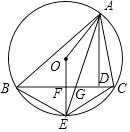17. 如图等边三角形ABC内接于圆，点P是圆上任意一点（P不与A、B、C重合），则∠APB= ．
18. 图中△ABC外接圆的圆心坐标是 ．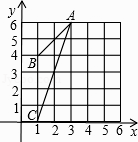
三、综合题
-
19. 如图，∠BAC的平分线交△ABC的外接圆于点D，∠ABC的平分线交AD于点E，
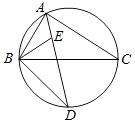(1)、求证：DE=DB；(2)、若∠BAC=90°，BD=4，求△ABC外接圆的半径．20. 如图，在△ABP中，C是BP边上一点，∠PAC=∠PBA，⊙O是△ABC的外接圆，AD是⊙O的直径，且交BP于点E．
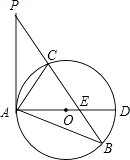(1)、求证：PA是⊙O的切线；(2)、过点C作CF⊥AD，垂足为点F，延长CF交AB于点G，若AG•AB=12，求AC的长．
