人教版数学九年级上册第24章 24.1.4圆周角 同步练习
试卷更新日期：2017-08-25 类型：同步测试
一、单选题
-
1. 如图，⊙O中，弦AB，CD相交于点P，∠A=42°，∠APD=77°，则∠B的大小是（ ）
A、43° B、35° C、34° D、44°2. 如图，⊙O的半径为3，四边形ABCD内接于⊙O，连接OB、OD，若∠BOD=∠BCD，则 的长为（ ）
A、π B、 C、2π D、3π3. 如图，▱ABCD中，∠B=70°，BC=6，以AD为直径的⊙O交CD于点E，则 的长为（ ）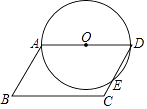
A、 π B、 π C、 π D、 π4. 如图，点A、B、C在⊙O上，AC∥OB，∠BAO=25°，则∠BOC的度数为（ ）
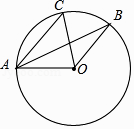A、25° B、50° C、60° D、80°5. 如图，AB是⊙O的直径，点C，D，E在⊙O上，若∠AED=20°，则∠BCD的度数为（ ）
A、100° B、110° C、115° D、120°6. 如图，⊙O的直径AB垂直于弦CD，∠CAB=36°，则∠BCD的大小是（ ）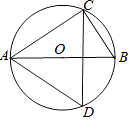
A、18° B、36° C、54° D、72°7. 如图，AB是⊙O的直径，CD是⊙O的弦，∠ACD=30°，则∠BAD为（ ）
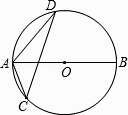A、30° B、50° C、60° D、70°8. 如图，在⊙O中，AB是直径，AC是弦，连接OC，若∠ACO=30°，则∠BOC的度数是（ ）
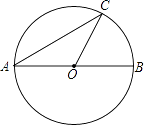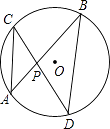
A、30° B、45° C、55° D、60°9. 如图，四边形ABCD为⊙O的内接四边形．延长AB与DC相交于点G，AO⊥CD，垂足为E，连接BD，∠GBC=50°，则∠DBC的度数为（ ）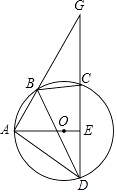
A、50° B、60° C、80° D、90°10. 如图是某商品的标志图案，AC与BD是⊙O的两条直径，首尾顺次连接点A，B，C，D，得到四边形ABCD．若AC=10cm，∠BAC=36°，则图中阴影部分的面积为（ ）
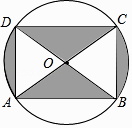A、5πcm2 B、10πcm2 C、15πcm2 D、20πcm211. 如图，AB是⊙O的直径，C，D是⊙O上位于AB异侧的两点．下列四个角中，一定与∠ACD互余的角是（ ）
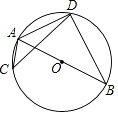A、∠ADC B、∠ABD C、∠BAC D、∠BAD12. 如图，已知⊙O为四边形ABCD的外接圆，O为圆心，若∠BCD=120°，AB=AD=2，则⊙O的半径长为（ ）
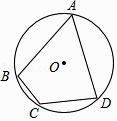A、 B、 C、 D、二、填空题
-
13.
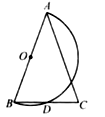
如图，已知在 中， ．以 为直径作半圆 ，交 于点 ．若 ，则 的度数是度．
14. 如图，△ABC内接于⊙O，∠ACB=90°，∠ACB的角平分线交⊙O于D．若AC=6，BD=5 ，则BC的长为 ．
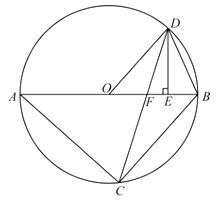
15. 如图，在⊙O 中，已知∠AOB=120°，则∠ACB= ．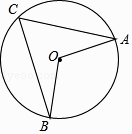
16. 如图，AB是半圆直径，半径OC⊥AB于点O，D为半圆上一点，AC∥OD，AD与OC交于点E，连结CD、BD，给出以下三个结论：①OD平分∠COB；②BD=CD；③CD2=CE•CO，其中正确结论的序号是 ．
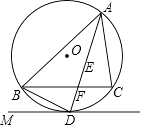
17. 如图，在Rt△ABC中，∠BAC=30°，以直角边AB为直径作半圆交AC于点D，以AD为边作等边△ADE，延长ED交BC于点F，BC=2 ，则图中阴影部分的面积为 ． （结果不取近似值）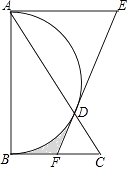
18. 如图，已知AM为⊙O的直径，直线BC经过点M，且AB=AC，∠BAM=∠CAM，线段AB和AC分别交⊙O于点D、E，∠BMD=40°，则∠EOM= ．
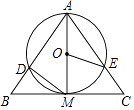19. 如图，⊙O是△ABC的外接圆，∠AOB=70°，AB=AC，则∠ABC= ．
20. 如图，已知⊙O是△ABC的外接圆，连接AO，若∠B=40°，则∠OAC=°．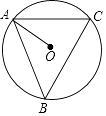
21. 如图，⊙O的内接四边形ABCD中，∠A=115°，则∠BOD等于 ．
三、解答题
-
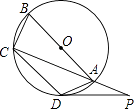
22. 如图，四边形ABCD内接于⊙O，AB是⊙O的直径，点P在CA的延长线上，∠CAD=45°．
（Ⅰ）若AB=4，求 的长；
（Ⅱ）若 = ，AD=AP，求证：PD是⊙O的切线．
23. 如图，点E是△ABC的内心，AE的延长线交BC于点F，交△ABC的外接圆⊙O于点D，连接BD，过点D作直线DM，使∠BDM=∠DAC．（Ⅰ）求证：直线DM是⊙O的切线；
（Ⅱ）求证：DE2=DF•DA．
