安徽省安庆市第十四中教育集团2019-2020学年九年级下学期月考试卷
试卷更新日期:2020-03-19 类型:月考试卷
一、选择题(本大题共10小题,每小题4分,共40分)
-
1. 如果反比例函数y= 的图像经过点P(-2,3),那么k的值是( )A、-6 B、 C、 D、62. 如图,已知在△ABC中,点D,E,F分别是边AB,AC,BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么CF:CB等于( )
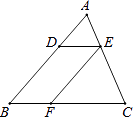 A、5:8 B、3:8 C、3:5 D、2:53. 如图,△ABC内接于⊙O, 若∠OAB=28°,则∠C的大小为( )
A、5:8 B、3:8 C、3:5 D、2:53. 如图,△ABC内接于⊙O, 若∠OAB=28°,则∠C的大小为( )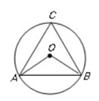 A、28° B、56° C、60° D、62°4. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:
A、28° B、56° C、60° D、62°4. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论: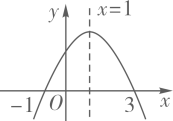
①a>0。②该函数的图象关于直线x=1对称。
③当x=-1或x=3时,函数y的值都等于0。
其中正确结论的个数是( )
A、3 B、2 C、1 D、05. 抛物线y=-3(x-4)2向右平移3个单位长度得到的抛物线对应的函数关系式为( )A、y=-3(x-7)2 B、y=-3(x-1)2 C、y=-3(x-4)2+3 D、y=-3(x-4)2-36. 河堤横断面如图所示,堤高=6米,迎水坡的坡比为1: ,则迎水坡的长为( )
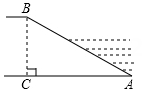 A、12 B、4 米 C、5 米 D、6 米7. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=12,点D在边BC上,点E在线段AD上,EF⊥AC于点F,EG⊥EF交AB于点G,若EF=EG,则CD的长为( )
A、12 B、4 米 C、5 米 D、6 米7. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=12,点D在边BC上,点E在线段AD上,EF⊥AC于点F,EG⊥EF交AB于点G,若EF=EG,则CD的长为( )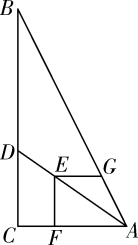 A、3.6 B、4 C、4.8 D、58. 如图,已知在Rt△ABC中,∠BAC=90°,AC=4,BC=5,若把Rt△ABC绕直线AC旋转一周,则所得圆锥的侧面积等于( )
A、3.6 B、4 C、4.8 D、58. 如图,已知在Rt△ABC中,∠BAC=90°,AC=4,BC=5,若把Rt△ABC绕直线AC旋转一周,则所得圆锥的侧面积等于( )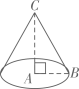 A、9π B、12π C、15π D、20π9. 函数y=x+m与y= (m≠0)在同一坐标系内的图像可以是( )A、
A、9π B、12π C、15π D、20π9. 函数y=x+m与y= (m≠0)在同一坐标系内的图像可以是( )A、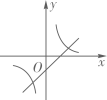 B、
B、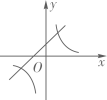 C、
C、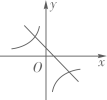 D、
D、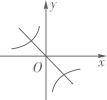 10. 如图,正方形ABCD的边长为2,P为CD的中点,连结AP,过点B作BE⊥AP于点E,延长CE交AD于点F,过点C作CH⊥BE于点G,交AB于点H,连接HF。下列结论正确的是( )
10. 如图,正方形ABCD的边长为2,P为CD的中点,连结AP,过点B作BE⊥AP于点E,延长CE交AD于点F,过点C作CH⊥BE于点G,交AB于点H,连接HF。下列结论正确的是( )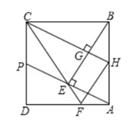 A、CE= B、EF= C、cos∠CEP= D、HF2=EF·CF
A、CE= B、EF= C、cos∠CEP= D、HF2=EF·CF二、填空题(本大题有4个小题,每小题5分,共20分)
-
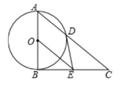
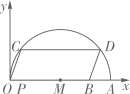
11. 如图,已知点A的坐标是(10,0),点B的坐标为(8,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标是。
 12. 如图,在平面直角坐标系中,抛物线y=-x2+3x+2与y轴交于点A,点B是拋物线的顶点,点C与点A是抛物线上的两个对称点,点D在x轴上运动,则四边形ABCD的两条对角线的长度之和的最小值为。
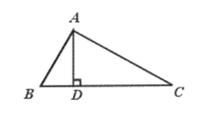
12. 如图,在平面直角坐标系中,抛物线y=-x2+3x+2与y轴交于点A,点B是拋物线的顶点,点C与点A是抛物线上的两个对称点,点D在x轴上运动,则四边形ABCD的两条对角线的长度之和的最小值为。 13. 如图,△ABC中,AD⊥BC于D,且有下列条件:
13. 如图,△ABC中,AD⊥BC于D,且有下列条件:①∠B+∠DAC=90°;
②∠B=∠DAC;
③
④AB2=BD·BC
其中一定能够判定△ABC是直角三角形的有(填序号)。
 14. 如图①,在矩形ABCD中,AB<AD,对角线AC,BD相交于点O,动点P由点A出发,沿AB→BC→CD向点D运动。设点P的运动路程为x,△AOP的面积为y,y与x的函数关系图象如图②所示,则AD边的长为。
14. 如图①,在矩形ABCD中,AB<AD,对角线AC,BD相交于点O,动点P由点A出发,沿AB→BC→CD向点D运动。设点P的运动路程为x,△AOP的面积为y,y与x的函数关系图象如图②所示,则AD边的长为。
三、解答题
-
15. 计算:|-2|+(sin36°- )0- +tan45°16. 已知:在△ABC中,AB=AC。
 (1)、求作:△ABC的外接圆。(要求:尺规作图,保留作图痕迹,不写作法)(2)、若△ABC的外接圆的圆心O到BC边的距离为4,BC=6,则⊙O的面积=。17. 如图,AC=8,分别以A、C为圆心,以长度5为半径作弧,两条弧分别相交于点B和D。依次连接A、B、C、D,连接BD交AC于点O。
(1)、求作:△ABC的外接圆。(要求:尺规作图,保留作图痕迹,不写作法)(2)、若△ABC的外接圆的圆心O到BC边的距离为4,BC=6,则⊙O的面积=。17. 如图,AC=8,分别以A、C为圆心,以长度5为半径作弧,两条弧分别相交于点B和D。依次连接A、B、C、D,连接BD交AC于点O。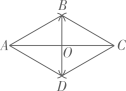 (1)、判断四边形ABCD的形状并说明理由;(2)、求BD的长。18. 如图,在⊙O中,半径OA与弦BD垂直,点C在⊙O上,∠AOB=80°
(1)、判断四边形ABCD的形状并说明理由;(2)、求BD的长。18. 如图,在⊙O中,半径OA与弦BD垂直,点C在⊙O上,∠AOB=80°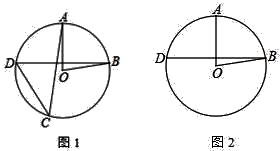 (1)、若点C在优弧BD上,求∠ACD的大小;(2)、若点C在劣弧BD上,直接写出∠ACD的大小.19. 某手机专营店,第一期进了甲种手机50部.售后统计,甲种手机的平均利润是160元/部.调研发现:甲种手机每增加1部,平均利润减少2元/部;该店计划第二期进货甲种手机比第一期增加x部,(1)、第二期甲种手机售完后的利润为8400元,那么甲种手机比第一期要增加多少部?(2)、当x取何值时,第二期进的甲种手机售完后获得的利润W最大,最大利润是多少?20. 图①是放置在水平面上的台灯,图②是其侧面示意图(台灯底座高度忽略不计),其中灯臂AC=40cm,灯罩CD=30cm,灯臂与底座构成的∠CAB=60°。CD可以绕点c上下调节一定的角度.使用发现:当CD与水平线所成的角为30°时,台灯光线最佳.现测得点D到桌面的距离为49.6cm。请通过计算说明此时台灯光线是否为最佳?(参考数据: 取1.73)。
(1)、若点C在优弧BD上,求∠ACD的大小;(2)、若点C在劣弧BD上,直接写出∠ACD的大小.19. 某手机专营店,第一期进了甲种手机50部.售后统计,甲种手机的平均利润是160元/部.调研发现:甲种手机每增加1部,平均利润减少2元/部;该店计划第二期进货甲种手机比第一期增加x部,(1)、第二期甲种手机售完后的利润为8400元,那么甲种手机比第一期要增加多少部?(2)、当x取何值时,第二期进的甲种手机售完后获得的利润W最大,最大利润是多少?20. 图①是放置在水平面上的台灯,图②是其侧面示意图(台灯底座高度忽略不计),其中灯臂AC=40cm,灯罩CD=30cm,灯臂与底座构成的∠CAB=60°。CD可以绕点c上下调节一定的角度.使用发现:当CD与水平线所成的角为30°时,台灯光线最佳.现测得点D到桌面的距离为49.6cm。请通过计算说明此时台灯光线是否为最佳?(参考数据: 取1.73)。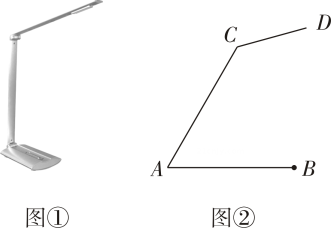 21. 家用电灭蚊器的发热部分使用了PTC发热材料,它的电阻R(kΩ)随温度t(℃)(在一定范围内)变化的大致图象如图所示.通电后,发热材料的温度在由室温10℃上升到30℃的过程中,电阻与温度成反例关系,且在温度达到30℃时,电阻下降到最小值;随后电阻承温度升高而增加,温度每上升1℃,电阻增加 kΩ.
21. 家用电灭蚊器的发热部分使用了PTC发热材料,它的电阻R(kΩ)随温度t(℃)(在一定范围内)变化的大致图象如图所示.通电后,发热材料的温度在由室温10℃上升到30℃的过程中,电阻与温度成反例关系,且在温度达到30℃时,电阻下降到最小值;随后电阻承温度升高而增加,温度每上升1℃,电阻增加 kΩ.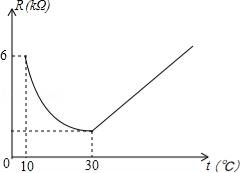 (1)、求R和t之间的关系式;(2)、家用电灭蚊器在使用过程中,温度在什么范围内时,发热材料的电阻不超过4kΩ.
(1)、求R和t之间的关系式;(2)、家用电灭蚊器在使用过程中,温度在什么范围内时,发热材料的电阻不超过4kΩ.