江西省萍乡市2018-2019学年七年级下学期数学期中考试试卷
试卷更新日期:2020-03-19 类型:期中考试
一、单选题
-
1. 以下列长度的三条线段为边,能构成三角形的是( )A、7,8,15 B、15,20,4 C、7,6,18 D、6,7,52. 若 ,则( )A、 , B、 , C、 , D、 ,3. 如图, ,则 的度数是( )度
 A、 B、 C、 D、4. 已知 , ,则 的值是( )A、 B、 C、 D、5. 计算下列各式① ② ③ ④ 正确有( )题A、 B、 C、 D、6. 在锐角三角形 中, , 分别是 , 边上的高,且 , 交于点 ,若 ,则 的度数是( )A、 B、 C、 D、7. 长方形的周长为 ,其中一边长为 ,面积为 则长方形中 与 的关系式为( )A、 B、 C、 D、8. 下列四幅图象近似刻画两个变量之间的关系,请按图象顺序将下面四种情景与之对应排序( )
A、 B、 C、 D、4. 已知 , ,则 的值是( )A、 B、 C、 D、5. 计算下列各式① ② ③ ④ 正确有( )题A、 B、 C、 D、6. 在锐角三角形 中, , 分别是 , 边上的高,且 , 交于点 ,若 ,则 的度数是( )A、 B、 C、 D、7. 长方形的周长为 ,其中一边长为 ,面积为 则长方形中 与 的关系式为( )A、 B、 C、 D、8. 下列四幅图象近似刻画两个变量之间的关系,请按图象顺序将下面四种情景与之对应排序( )
①一辆汽车在公路上匀速行驶(汽车行驶的路程与时间的关系)
②向锥形瓶中匀速注水(水面的高度与注水时间的关系)
③将常温下的温度计插入一杯热水中(温度计的读数与时间的关系)
④一杯越来越凉的水(水温与时间的关系)
A、③②④① B、③④②① C、①④②③ D、①②③④二、填空题
-
9. 计算: =.10. 纳米 米, 纳米用科学记数法表示为米.11. 一个长方体的长、宽、高分别是3x-4,2x和x,它的体积等于12. 若 ,则 , .13. 一个角的余角等于这个角的 ,这个角的度数为.14. 如图,将一副三角板摆成如图所示,图中 .
 15. 如图,已知 , , 平分 , ,则 .
15. 如图,已知 , , 平分 , ,则 . 16. 将4个数a,b,c,d排成2行、2列,两边各加一条竖直线记成 ,定义 =ad﹣bc,上述记号就叫做2阶行列式.若 ,则x= .
16. 将4个数a,b,c,d排成2行、2列,两边各加一条竖直线记成 ,定义 =ad﹣bc,上述记号就叫做2阶行列式.若 ,则x= .三、解答题
-
17. 计算18. 先化简,再求值, 其中19. 已知 ,求 的值20. 作图题:如图,已知 , ( )求作一个角使它等于 (不写作法,保留作图痕迹,不在原图上作)
 21. 在三角形中, 是边 上的中线, , ,求 与 的周长之差.
21. 在三角形中, 是边 上的中线, , ,求 与 的周长之差.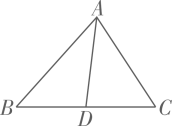 22. 如图, , , .请说明 是 的平分线。
22. 如图, , , .请说明 是 的平分线。
解:理由如下: ,
,()
,()
,()
又 ,()
,()
平分
23. 如图,在三角形ABC中, ,垂足为 ,过点 作 交 于 ,作 交 于 ,交 于 ,若 ,求 和 的度数.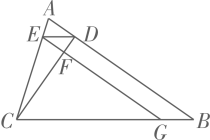 24. 已知△ABC的面积是 , ,在 边上有一动点 ,连接 ,设 为 , 面积为 .
24. 已知△ABC的面积是 , ,在 边上有一动点 ,连接 ,设 为 , 面积为 . (1)、求 与 之间的关系式(2)、用表格表示当 从 时到 时(每次增加 ), 的对应值.(3)、当 时, 的值等于多少?此时说明了什么?25. 为了迎接2022年北京冬奥会,萍乡外国语学校组织了一次大型长跑比赛。甲,乙两人在比赛时,路程 (米)与时间 (分钟)的关系如图所示,极据图像解答下列问题:
(1)、求 与 之间的关系式(2)、用表格表示当 从 时到 时(每次增加 ), 的对应值.(3)、当 时, 的值等于多少?此时说明了什么?25. 为了迎接2022年北京冬奥会,萍乡外国语学校组织了一次大型长跑比赛。甲,乙两人在比赛时,路程 (米)与时间 (分钟)的关系如图所示,极据图像解答下列问题: (1)、这次长跑比赛的全程是米;先到达终点的人比另一个人领先分钟:(2)、乙是学校田径队运动员,十分注意比赛技巧,比赛过程分起跑、途中跑冲刺跑三阶段,经历了两次加速过程.问第 分钟时乙还落后甲多少米?(3)、假设乙在第一次加速后,始终保持这个速度继续前进。那么甲,乙两人谁先到达终点?请说明理由.(4)、事实上乙追上甲的时间是多少分钟?
(1)、这次长跑比赛的全程是米;先到达终点的人比另一个人领先分钟:(2)、乙是学校田径队运动员,十分注意比赛技巧,比赛过程分起跑、途中跑冲刺跑三阶段,经历了两次加速过程.问第 分钟时乙还落后甲多少米?(3)、假设乙在第一次加速后,始终保持这个速度继续前进。那么甲,乙两人谁先到达终点?请说明理由.(4)、事实上乙追上甲的时间是多少分钟?