江西省高安市2018-2019学年七年级下学期数学期中考试试卷

试卷更新日期：2020-03-19 类型：期中考试

进入出卷网下载

一、单选题

1. $\sqrt{81}$ 的算术平方根是（）

A、9 B、±9 C、±3 D、3

查看试题解析
2. 若点P在第二象限，且点P到x轴的距离为3，到y轴的距离为2，则点P的坐标为(　　)

A、(－3，2) B、(－2，3) C、(3，－2) D、(2，－3)

查看试题解析
3. 若方程组 ${\begin{array}{l} x + y = ☆ \\ 2 x + y = 16 \end{array}$ 的解为 ${\begin{array}{l} x = 6 \\ y = □ \end{array}$ ，则被“☆”、“□”遮住的两个数分别是(　　)

A、10，3 B、3，10 C、4，10 D、10，4

查看试题解析
4. 将一直角三角板与两边平行的纸条按如图所示的方式放置，有下列结论：（1） $∠ 1 = ∠ 2$ ；（2） $∠ 3 = ∠ 4$ ；（3） $∠ 2 + ∠ 4 = 90 °$ ；（4） $∠ 4 + ∠ 5 = 180 °$ .其中正确个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 若x，y满足|x﹣5|+ $\sqrt{x + 2 y + 1}$ ＝0，则 $\sqrt{x + y}$ 的值是(　 )

A、1 B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、 $\sqrt{5}$

查看试题解析
6. 已知点E(x₀ ， y₀)，F(x₂ ， y₂)，点M(x₁ ， y₁)是线段EF的中点，则 $x_{1} = \frac{x_{0} + x_{2}}{2} ， y_{1} = \frac{y_{0} + y_{2}}{2}$ .在平面直角坐标系中有三个点A(1，－1)，B(－1，－1)，C(0，1)，点P(0，2)关于A的对称点为P₁(即P，A，P₁三点共线，且PA＝P₁A)，P₁关于B的对称点为P₂ ， P₂关于C的对称点为P₃ ，按此规律继续以A，B，C为对称点重复前面的操作，依次得到P₄ ， P₅ ， P₆ ， …，则点P₂₀₁₉的坐标是(　　)

A、(4，0) B、(-2，2) C、(2，－4) D、(－4，2)

查看试题解析

二、填空题

7. 在平面直角坐标系内，把点A(4，﹣1)先向右平移3个单位长度，再向上平移2个单位长度得到点A′，则点A′的坐标是．

查看试题解析
8. 若(a+6)x+y^|a|^﹣⁵=1是关于x、y的二元一次方程，则a的值是．

查看试题解析
9. 用“*”表示一种新运算：对于任意正实数a，b，都有a*b＝ $\sqrt{b}$ ＋a，例如 4*9＝ $\sqrt{9}$ ＋4＝7，那么5*289＝．

查看试题解析
10. 如图，是用一张长方形纸条折成的，如果∠1=108°，那么∠2= °.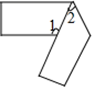

查看试题解析
11. 把命题“等角的补角相等”改写成“如果…那么…”的形式是．

查看试题解析
12. 已知，在同一平面内，∠ABC＝50°，AD∥BC，∠BAD的平分线交直线BC于点E，那么∠AEB的度数为．

查看试题解析

三、解答题

13. 计算： $- 2^{2} + \sqrt{4} - \sqrt[3]{\frac{8}{27}} \times 3 - | 1 - \sqrt{3} |$ .

查看试题解析
14. 解方程组 ${\begin{array}{l} x - 2 y = - 1 \\ 4 x + 3 y = 7 \end{array}$ .

查看试题解析
15. 如图所示，直线AB与直线CD交于点O，OE⊥AB，OF平分∠AOC，若∠BOD=70°．你能否求出∠DOF的度数吗？

查看试题解析
16. 如图，∠ADE=∠B，∠CDE=∠BFG，求证：FG∥CD．

查看试题解析
17. 在平面直角坐标系中，△ABC三个顶点的坐标分别是A(−2，2)、B(2，0)，C(−4，−2).

(1)、在平面直角坐标系中画出△ABC；

(2)、若将(1)中的△ABC平移，使点B的对应点B′坐标为(6，2)，画出平移后的△A′B′C′；

(3)、求△A′B′C′的面积.

查看试题解析
18. 如图，若∠ADE=∠ABC，BE⊥AC于E，MN⊥AC于N，试判断∠1与∠2的关系，并说明理由

查看试题解析
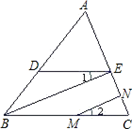19. 求下列代数式的值：

(1)、如果a²＝4，b的算术平方根为3，求a+b的值.

(2)、已知x是25的平方根，y是16的算术平方根，且x＜y，求x﹣y的值.

查看试题解析
20. 阅读第(1)题解答过程填理由，并解答第(2)题

(1)、已知：如图 1 AB∥CD，P 为 AB、CD 之间一点，求∠B+∠C+∠BPC的大小．
解：过点 P 作 PM∥AB

∵AB∥CD(已知)

∴PM∥CD

∴∠B+∠1=180°

∴∠C+∠2=180°

∵∠BPC=∠1+∠2

∴∠B+∠C+∠BPC=360°

(2)、我们生活中经常接触小刀，小刀刀柄外形是一个直角梯形(挖去一个小半圈)如图 2，刀片上、下是平行的，转动刀片时会形成∠1 和∠2，那么∠1+∠2 的大小是否会随刀片的转动面改变？说明理由．

查看试题解析
21. 在平面直角坐标系中，有点A(1，2a+1)，B(﹣a，a﹣3)．

(1)、当点A在第一象限的角平分线上时，求a的值；

(2)、当点B在到x轴的距离是到y轴的距离2倍时，求点B所在的象限位置；

(3)、若线段AB∥x轴，求三角形AOB的面积．

查看试题解析
22. 如图1所示，已知BC∥OA，∠B＝∠A＝120°

(1)、说明OB∥AC成立的理由．

(2)、如图2所示，若点E，F在BC上，且∠FOC＝∠AOC，OE平分∠BOF，求∠EOC的度数．

(3)、在（2）的条件下，若左右平移AC，如图3所示，那么∠OCB：∠OFB的比值是否随之发生变化？若变化，请说明理由；若不变，请求出这个比值．

(4)、在（3）的条件下，当∠OEB＝∠OCA时，求∠OCA的度数．

查看试题解析