江西省赣州市宁都县2018-2019学年七年级下学期数学期中考试试卷
试卷更新日期：2020-03-19 类型：期中考试
一、单选题
-
1. 如图，小手盖住的点的坐标可能是（ ）．
A、（﹣3，4）； B、（5，2） C、（﹣3，﹣6）； D、（6，﹣4）．2. 实数a、b在数轴上的位置如图所示，且|a|＞|b|，则化简 的结果为（ ）
A、2a+b B、-2a+b C、b D、2a-b3. 下列命题中是假命题的是（ ）．A、垂线段最短 B、相等的角是对顶角； C、同旁内角互补，两直线平行 D、在同一平面内，过一点有且只有一条直线与已知直线垂直．4. 如图，现将一块三角板的含有60°角的顶点放在直尺的一边上，若∠1=2∠2，那么∠1的度数为（ ）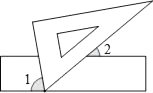
A、50° B、60° C、70° D、80°5. 在如图所示的四种沿AB进行折叠的方法中，不一定能判断纸带两条边a，b互相平行的是（ ）
A、如图1，展开后测得∠1=∠2 B、如图2，展开后测得∠1=∠2且∠3=∠4 C、如图3，测得∠1=∠2 D、在图④中，展开后测得∠1+∠2=180°6. 如图，在Rt△ABC中，∠ACB=90°，点D在AB边上，将△CBD沿CD折叠，使点B恰好落在AC边上的点E处，若∠A=26°，则∠CDE度数为（ ）．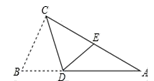
A、45°； B、64° ； C、71°； D、80°．二、填空题
-
7. 若 ，则 ．8. 如图，直线l1∥l2 ， ∠α=∠β，∠1=38°，则∠2=.
9. 如图，直线AB、CD相交于点O，EO⊥AB，垂足为点O，若∠AOD=131°，则∠EOC=°．
10. 如图，将△ABC沿BC方向平移1cm得到△DEF，若△ABC的周长等于10cm，则四边形ABFD的周长等于cm．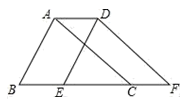
三、解答题
-
11. 若 的整数部分为a，小数部分为b，求 的值.12. 已知点A（2a＋1，a＋7）到x轴、y轴的距离相等，求a的值．13. 已知2a﹣1的算术平方根是5，a+b﹣2的平方根是±3，c+1是﹣8的立方根，求a+b+c的值．14.
直线a，b，c，d的位置如图所示，已知∠1=58°，∠2=58°，∠3=70°，求∠4的度数．
15. 如图，三角形ABO中，A（﹣2，﹣3）、B（2，﹣1），三角形A′B′O′是三角形ABO平移之后得到的图形，并且O的对应点O′的坐标为（4，3）．
(1)、求三角形ABO的面积；(2)、作出三角形ABO平移之后的图形三角形A′B′O′，并写出A′、B′两点的坐标分别为A′、B′；(3)、P（x，y）为三角形ABO中任意一点，则平移后对应点P′的坐标为 ．16. 完成下面推理过程：如图所示，直线AD与AB、CD分别相交于点A、D，与EC、BF分别相交于点H、G，已知：∠1=∠2，∠B=∠C．
求证：∠A=∠D．
证明：∵∠1=∠2（已知），∠2=∠AGB（对顶角相等）
∴∠1=∠AGB（）
∴EC∥BF（）
∴∠B=∠AEC（）
又∵∠B=∠C（已知）
∴∠AEC=（）
∴（）
∴∠A=∠D（）
17. 如图，已知点E、F在直线AB上，点G在线段CD上，ED与FG交于点H，∠C=∠EFG，∠CED=∠GHD．
(1)、求证：AB∥CD；(2)、若∠EHF=80°，∠D=40°，求∠AEM的度数。18.已知如图，DE⊥AC ， ∠AGF=∠ABC ， ∠1+∠2=180°，试判断BF与AC的位置关系，并说明理由．
19. 如图，EF∥AB，∠DCB＝70°，∠CBF＝20°，∠EFB＝130°，
(1)、问直线CD与AB有怎样的位置关系？并说明理由；(2)、若∠CEF＝70°，求∠ACB的度数．20. 如图，以直角三角形AOC 的直角顶点O为原点，以 OA，OC 所在直线为x轴，y轴建立平面直角坐标系，点 满足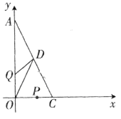
(1)、则 点的坐标为； 点的坐标为.(2)、直角三角形 的面积为.(3)、已知坐标轴上有两动点 同时出发， 点从 点出发沿 轴负方向以1个单位长度每秒的速度匀速移动， 点从 点出发以2个单位长度每秒的速度沿 轴正方向移动，点 到达 点整个运动随之结束． 的中点 的坐标是 ，设运动时间为t（t＞0）秒，问：是否存在这样的t使 ？若存在，请求出 的值；若不存在，请说明理由.21. 如图，在平面直角坐标系xOy中，已知A（6，0），B（8，6），将线段OA平移至CB，点D在x轴正半轴上（不与点A重合），连接OC、AB、CD、BD．
(1)、写出点C的坐标；(2)、当△ODC的面积是△ABD的面积的3倍时，求点D的坐标；(3)、设∠OCD=α，∠DBA=β，∠BDC=θ，判断α、β、θ之间的数量关系，并说明理由．