湖南省永州市新田县2017-2018学年七年级下学期数学期中考试试卷
试卷更新日期:2020-03-19 类型:期中考试
一、单选题
-
1. 下列方程组中不是二元一次方程组的是 ( )A、 B、 C、 D、2. 下列运算中,正确是( )A、 B、 C、 D、3. 下列多项式乘法,能用平方差公式进行计算的是( )A、 B、( C、 ) D、4. 方程组 的解为 ,则被遮盖的两个数分别为( )A、2,1 B、5,1 C、2,3 D、2,45. 下列由左到右的变形,属于因式分解的是( )A、 B、 C、 D、6. 计算(x+1)(x+2)的结果为( )A、x2+2 B、x2+3x+2 C、x2+3x+3 D、x2+2x+27. 下列各式中能用完全平方公式进行因式分解的是( )A、x2+x+1 B、x2+2x﹣1 C、x2﹣1 D、x2﹣6x+98. 因式分解x2y-4y的正确结果是( )A、y(x+2)(x-2) B、y(x+4)(x-4) C、y(x2-4) D、y(x-2)29. 从边长为 的大正方形纸板中挖去一个边长为 的小正方形纸板后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙)。那么通过计算两个图形阴影部分的面积,可以验证成立的公式为( )
 A、 B、 C、 D、10. 下表中,填在各正方形中的四个数之间都有相同的规律,根据此规律,m的值是( )
A、 B、 C、 D、10. 下表中,填在各正方形中的四个数之间都有相同的规律,根据此规律,m的值是( ) A、58 B、66 C、74 D、112
A、58 B、66 C、74 D、112二、填空题
-
11. 计算: =; = . (﹣2x3y2)•(3x2y)=12. 的公因式是 .13. 填空:x2+10x+ =(x+ )2 .14. 计算 的结果为 .15. 计算 . = .16. 明代珠算大师程大位著有《珠算统宗》一书,有下面的一道题:“隔墙听得客分银,不知人数不知银,七两分之多四两,九两分之少半斤(1斤等于16两)”.据此可知,客有人,银有两.17. 已知关于x,y的二元一次方程组 的解互为相反数,则k的值是 .18. 已知: ,则代数式: 的值为.
三、解答题
-
19. 请用指定的方法解下列方程组:(1)、 (代入消元法)(2)、 (加减消元法)20. 卫星绕地球的运动速度(第一宇宙速度)每秒为 米,一天大约是 秒,求卫星绕地球运行一天后所经过的路程(用科学记数法表示).21. 求代数式的值:(1)、已知 , ,求 的值.(2)、已知 , ,求 , 的值.22. 先化简再求值: ,其中, .23. 因式分解:(1)、(2)、24. 古运河是扬州的母亲河,为打造古运河风光带,现有一段长为180米的河道整治任务由 两工程队先后接力完成. 工作队每天整治12米, 工程队每天整治8米,共用时20天.
根据题意,甲、乙两名同学分别列出尚不完整的方程组如下:
甲:
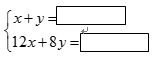
乙:
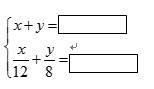 (1)、根据甲、乙两名同学所列的方程组,请你分别指出未知数 表示的意义.
(1)、根据甲、乙两名同学所列的方程组,请你分别指出未知数 表示的意义.甲: 表示 , 表示;
乙: 表示 , 表示 .
(2)、在方框中补全甲、乙两名同学所列的方程组.(3)、求 两工程队分别整治河道多少米.(写出完整的解答过程)25. 学校准备租用一批汽车,现有甲、乙两种大客车,甲种客车每辆载客量45人,乙种客车每辆载客量30人,已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.(1)、求1辆甲种客车和1辆乙种客车的租金分别是多少元?(2)、学校计划租用甲、乙两种客车共8辆,送330名师生集体外出活动,最节省的租车费用是多少?26. 阅读材料:把代数式通过配凑等手段得到局部完全平方式,再进行有关计算和解题,这种解题方法叫做配方法.
如(1)用配方法分解因式: .
解:原式=
= ;(2)M= ,利用配方法求M的最小值.
解:M=
=
M有最小值1.
请根据上述材料,解决下列问题:
(1)、在横线上添加一个常数,使之成为完全平方式:(2)、用配方法分解因式:(3)、若M= ,求M的最小值.