湖南省邵阳市邵阳县2017-2018学年七年级下学期数学期中考试试卷

试卷更新日期：2020-03-19 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程组是二元一次方程组的是（）

A、 ${\begin{cases} x - y = 1 \\ xy = 2 \end{cases}$ B、 $\overset{}{{\begin{cases} 4 x - y = - 1 \\ y = 2 x \end{cases}}$ C、 ${\begin{cases} x^{2} - x - 2 = 0 \\ y = x + 1 \end{cases}$ D、 ${\begin{array}{l} \frac{1}{x} - 1 = y \\ 3 x + y = 0 \end{array}$

查看试题解析
2. 方程组 ${\begin{array}{l} 3 x - 2 y = 5 ， \\ 5 x + 4 y = 1 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 1 ， \\ y = 1 \end{array}$ B、 ${\begin{array}{l} x = 1 ， \\ y = - 1 \end{array}$ C、 ${\begin{array}{l} x = 2 ， \\ y = \frac{1}{2} \end{array}$ D、 ${\begin{array}{l} x = \frac{1}{3} ， \\ y = - 2 \end{array}$

查看试题解析
3. 在a•（）=a⁴中，括号内的代数式应为（）

A、 $a^{2}$ B、 $a^{3}$ C、 $a^{4}$ D、 $a^{5}$

查看试题解析
4. 若x，y为正整数，且2^x•2^2y=2⁹ ，则x，y的值有（）

A、1对 B、2对 C、3对 D、4对

查看试题解析
5. 下列各式由左到右的变形中，属于因式分解的是（）

A、 $10 x^{2} - 5 x = 5 x (2 x - 1)$ B、 $a^{2} - b^{2} - c^{2} = (a - b) (a + b) - c^{2}$ C、 $a (m + n) = am + an$ D、 $x^{2} - 16 + 6 x = (x + 4) (x - 4) + 6 x$

查看试题解析
6. 若x-2和x+3是多项式x²+mx+n仅有的两个因式，则mn的值为（）

A、1 B、 $- 1$ C、 $- 6$ D、6

查看试题解析
7. 若x、y满足方程组 ${\begin{matrix} x + 3 y = 7 \\ 3 x + y = 5 \end{matrix}$ ，则x﹣y的值等于（）

A、﹣1 B、1 C、2 D、3

查看试题解析
8. 已知 ${\begin{cases} 4x - 5 y + 2 z = 0 \\ x + 4 y - 3 z = 0 \end{cases}$ (xyz≠0)，则x：y：z的值为（）

A、1：2：3 B、3：2：1 C、2：1：3 D、不能确定

查看试题解析
9. 小林买了7本数学书和2本语文书共花了100元；小敏买了4本语文书和2本数学书共花了80元，则买2本数学书和1本语文书要花（）

A、25元 B、30元 C、35元 D、45元

查看试题解析
10. 若4x²+(k-1)x+9能用完全平方公式因式分解，则k的值为（）

A、 $\pm 6$ B、 $\pm 12$ C、 $- 13$ 或11 D、13或 $- 11$

查看试题解析

二、填空题

11. (-x)•x²•(-x)⁶= ．

查看试题解析
12. 已知二元一次方程5x-2y=14，用含x的代数式表示y，则y= ．

查看试题解析
13. 若 ${\begin{cases} x = a \\ y = b \end{cases}$ 是方程3x+y=1的解，则9a+3b+1= ．

查看试题解析
14. (-3)²⁰¹⁹×(- $\frac{1}{3}$ )²⁰¹⁸= ．

查看试题解析
15. 将多项式xy²-16x因式分解；其结果是．

查看试题解析
16. 如果(2x+2y+1)(2x+2y-1)=15，那么x+y的值是．

查看试题解析
17. 已知代数式-3x^m-1y³与2xⁿy^m+n是同类项，则-3x^m-1y³与2xⁿy^m+n的积是．

查看试题解析
18. 如图，正方形卡片A类、B类和长方形卡片C类各若干张，如果要拼一个长为(a+2b)，宽为(2a+b)的大长方形，那么需要A类、B类和C类卡片的张数分别为．

查看试题解析

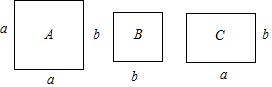
三、解答题

19. 解方程组

(1)、 ${\begin{array}{l} y = 1 - x ， & ① \\ 5 x + 2 y = 8 ； & ② \end{array}$

(2)、 ${\begin{array}{l} \frac{x + 1}{3} = 2 y ， & ① \\ 2 (x + 1) - y = 11 ． & ② \end{array}$

查看试题解析
20. 求值

(1)、先化简再求值：5x²-(x-2)(3x+1)-2(x+1)(x-5)，其中x=-1．

(2)、已知a+b=4，ab=2，求a³b+2a²b²+ab³的值．

查看试题解析
21. 已知多项式x²-mx+n与x-2的乘积中不含x²项和x项，试求m和n的值，并求这两个多项式的乘积．

查看试题解析
22. 已知a²+b²=13，a+b=1，且b＞a，求a-b的值．

查看试题解析
23. 观察下列等式：
(x-1)(x+1)=x²-1；

(x-1)(x²+x+1)=x³-1

(x-1)(x³+x²+x+1)=x⁴-1

(x-1)(x⁴+x³+x²+x+1)=x⁵-1；

……

(1)、猜想(x-1)(xⁿ+x^n-1+x^n-2+…+x+1)= ．

(2)、2¹⁹+2¹⁸+2¹⁷+…+2³+2²+2+1．

(3)、5²⁰¹⁸+5²⁰¹⁷+5²⁰¹⁶+…+5³+5²+5+1．

查看试题解析
24. 把下列多项式因式分解

(1)、6a²+12ab+6b²

(2)、2a(x²+4)²-32ax² ．

查看试题解析
25. “鸡兔同笼”是我国古代著名的数学趣题之一．大约在1500年前成书的《孙子算经》中，就有关于“鸡兔同笼”的记载：“今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？”这四句话的意思是：有若干只鸡兔关在一个笼子里，从上面数，有35个头；从下面数，有94条腿．问笼中各有几只鸡和兔？

查看试题解析