江西省赣州市宁都县2018-2019学年九年级下学期数学期中考试试卷
试卷更新日期:2020-03-19 类型:期中考试
一、单选题
-
1. -4的相反数是( )A、 B、 C、4 D、-42. 下列计算正确是( )A、2a2﹣a2=1 B、(ab)2=ab2 C、a2+a3=a5 D、(a2)3=a63. 测试五位学生的“一分钟跳绳”成绩,得到五个各不相同的数据,在统计时出现了一处不符合题意:将最高成绩写得更高了,则计算结果不受影响的是( )A、中位数 B、平均数 C、方差 D、极差4. 如图是由5个相同的正方体搭成的几何体,其左视图是( )
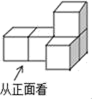 A、
A、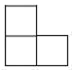 B、
B、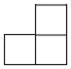 C、
C、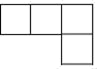 D、
D、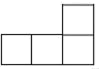 5. 如图,在平面直角坐标系中,函数 y = kx 与 y = - 的图象交于 A、B 两点,过 A 作 y 轴的垂线,交函数 的图象于点 C,连接 BC,则△ABC 的面积为( )
5. 如图,在平面直角坐标系中,函数 y = kx 与 y = - 的图象交于 A、B 两点,过 A 作 y 轴的垂线,交函数 的图象于点 C,连接 BC,则△ABC 的面积为( )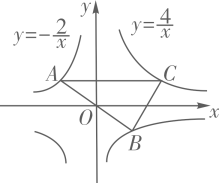 A、2 B、4 C、6 D、86. 已知关于x的一元二次方程(a+1)x2+2bx+(a+1)=0有两个相等的实数根,下列判断正确是( )A、1一定不是关于x的方程x2+bx+a=0的根 B、0一定不是关于x的方程x2+bx+a=0的根 C、1和﹣1都是关于x的方程x2+bx+a=0的根 D、1和﹣1不都是关于x的方程x2+bx+a=0的根
A、2 B、4 C、6 D、86. 已知关于x的一元二次方程(a+1)x2+2bx+(a+1)=0有两个相等的实数根,下列判断正确是( )A、1一定不是关于x的方程x2+bx+a=0的根 B、0一定不是关于x的方程x2+bx+a=0的根 C、1和﹣1都是关于x的方程x2+bx+a=0的根 D、1和﹣1不都是关于x的方程x2+bx+a=0的根二、填空题
-
7. 若式子 在实数范围内有意义,则x的取值范围是 .
8. 我国自主研发的某型号手机处理器采用10 nm工艺,已知1 nm=0.000000001 m,则10 nm用科学记数法可表示为m.9. 不等式组 的解集为 .
10. 如图,扇形的半径为3,圆心角θ为120°,用这个扇形围成一个圆锥的侧面,所得圆锥的底面半径为 . 11. 如图,每个图案均由边长相等的黑、白两色正方形按规律拼接而成,照此规律,第n个图案中白色正方形比黑色正方形多个.(用含n的代数式表示)
11. 如图,每个图案均由边长相等的黑、白两色正方形按规律拼接而成,照此规律,第n个图案中白色正方形比黑色正方形多个.(用含n的代数式表示)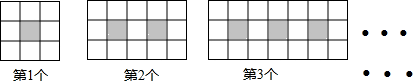 12. 如图,在平面直角坐标系中,O 为坐标原点,四边形 ABCD 是平行四边形,点 A、B、C 的坐标分别为 A(0,4),B(﹣2,0),C(8,0),点 E 是 BC的中点,点 P 为线段 AD 上的动点,若△BEP 是以 BE 为腰的等腰三角形,则点 P 的坐标为 .
12. 如图,在平面直角坐标系中,O 为坐标原点,四边形 ABCD 是平行四边形,点 A、B、C 的坐标分别为 A(0,4),B(﹣2,0),C(8,0),点 E 是 BC的中点,点 P 为线段 AD 上的动点,若△BEP 是以 BE 为腰的等腰三角形,则点 P 的坐标为 .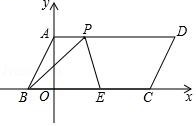
三、解答题
-
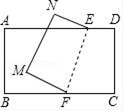
13.(1)、计算:﹣14﹣2×(﹣3)2+ ÷(﹣ )(2)、如图,小林将矩形纸片ABCD沿折痕EF翻折,使点C、D分别落在点M、N的位置,发现∠EFM=2∠BFM,求∠EFC的度数.
 14. 先化简,再求值: ,其中m= +1.15. 请你仅用无刻度的直尺在下面的图中作出△ABC 的边 AB 上的高 CD.
14. 先化简,再求值: ,其中m= +1.15. 请你仅用无刻度的直尺在下面的图中作出△ABC 的边 AB 上的高 CD.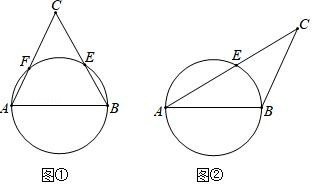 (1)、如图①,以等边三角形 ABC 的边 AB 为直径的圆,与另两边 BC、AC 分别交于点 E、F.(2)、如图②,以钝角三角形 ABC 的一短边 AB 为直径的圆,与最长的边 AC 相交于点 E.16. 已知某初级中学九(1)班共有40名同学,其中有22名男生,18名女生.(1)、若随机选一名同学,求选到男生的概率.(2)、学校因组织考试,将小明、小林随机编入A、B、C三个考场,请你用画树状图法或列表法求两人编入同一个考场的概率.17. 徐州至北京的高铁里程约为700km,甲、乙两人从徐州出发,分别乘坐“徐州号”高铁A与“复兴号”高铁B前往北京.已知A车的平均速度比B车的平均速度慢80km/h,A车的行驶时间比B车的行驶时间多40%,两车的行驶时间分别为多少?18. 在“书香校园”活动中,某校为了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成部分统计图表如下:
(1)、如图①,以等边三角形 ABC 的边 AB 为直径的圆,与另两边 BC、AC 分别交于点 E、F.(2)、如图②,以钝角三角形 ABC 的一短边 AB 为直径的圆,与最长的边 AC 相交于点 E.16. 已知某初级中学九(1)班共有40名同学,其中有22名男生,18名女生.(1)、若随机选一名同学,求选到男生的概率.(2)、学校因组织考试,将小明、小林随机编入A、B、C三个考场,请你用画树状图法或列表法求两人编入同一个考场的概率.17. 徐州至北京的高铁里程约为700km,甲、乙两人从徐州出发,分别乘坐“徐州号”高铁A与“复兴号”高铁B前往北京.已知A车的平均速度比B车的平均速度慢80km/h,A车的行驶时间比B车的行驶时间多40%,两车的行驶时间分别为多少?18. 在“书香校园”活动中,某校为了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成部分统计图表如下:类别
家庭藏书m本
学生人数
A
0≤m≤25
20
B
26≤m≤100
a
C
101≤m≤200
50
D
m≥201
66
根据以上信息,解答下列问题:
(1)、该调查的样本容量为 , a=;(2)、在扇形统计图中,“A”对应扇形的圆心角为°;(3)、若该校有2000名学生,请估计全校学生中家庭藏书200本以上的人数.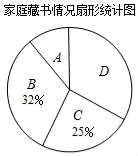 19. 日照间距系数反映了房屋日照情况.如图①,当前后房屋都朝向正南时,日照间距系数=L:(H﹣H1),其中L为楼间水平距离,H为南侧楼房高度,H1为北侧楼房底层窗台至地面高度.
19. 日照间距系数反映了房屋日照情况.如图①,当前后房屋都朝向正南时,日照间距系数=L:(H﹣H1),其中L为楼间水平距离,H为南侧楼房高度,H1为北侧楼房底层窗台至地面高度.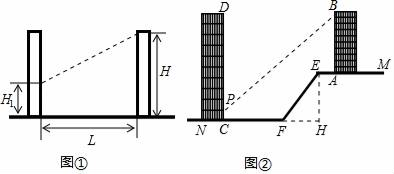
如图②,山坡EF朝北,EF长为15m,坡度为i=1:0.75,山坡顶部平地EM上有一高为22.5m的楼房AB,底部A到E点的距离为4m.
(1)、求山坡EF的水平宽度FH;(2)、欲在AB楼正北侧山脚的平地FN上建一楼房CD,已知该楼底层窗台P处至地面C处的高度为0.9m,要使该楼的日照间距系数不低于1.25,底部C距F处至少多远?20. 如图,在矩形ABCD中,AD=4,点E在边AD上,连接CE,以CE为边向右上方作正方形CEFG,作FH⊥AD,垂足为H,连接AF.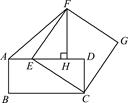 (1)、求证:FH=ED;(2)、当AE为何值时,△AEF的面积最大?21. 如图,AB是⊙O的直径,点C在⊙O上,AD垂直于过点C的切线,垂足为D,CE垂直AB,垂足为E.延长DA交⊙O于点F,连接FC,FC与AB相交于点G,连接OC.
(1)、求证:FH=ED;(2)、当AE为何值时,△AEF的面积最大?21. 如图,AB是⊙O的直径,点C在⊙O上,AD垂直于过点C的切线,垂足为D,CE垂直AB,垂足为E.延长DA交⊙O于点F,连接FC,FC与AB相交于点G,连接OC.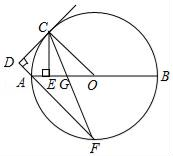 (1)、求证:CD=CE;(2)、若AE=GE,求证:△CEO是等腰直角三角形.22. 如图,已知抛物线y= x2﹣ x﹣n(n>0)与x轴交于A,B两点(A点在B点的左边),与y轴交于点C.
(1)、求证:CD=CE;(2)、若AE=GE,求证:△CEO是等腰直角三角形.22. 如图,已知抛物线y= x2﹣ x﹣n(n>0)与x轴交于A,B两点(A点在B点的左边),与y轴交于点C.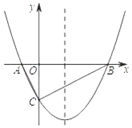 (1)、若AB=4,求n的值;(2)、如图,若△ABC为直角三角形,求n的值;(3)、如图,在(2)的条件下,若点P在抛物线上,点Q在抛物线的对称轴上,是否存在以点B、C、P、Q为顶点的四边形是平行四边形?若存在,请求P点的坐标;若不存在,请说明理由.23. 在学习了矩形这节内容之后,明明同学发现生活中的很多矩形都很特殊,如我们的课本封面、A4 的打印纸等,这些矩形的长与宽之比都为 :1,我们将具有这类特征的矩形称为“完美矩形”如图(1),在“完美矩形”ABCD 中,点 P 为 AB 边上的定点,且 AP=AD.
(1)、若AB=4,求n的值;(2)、如图,若△ABC为直角三角形,求n的值;(3)、如图,在(2)的条件下,若点P在抛物线上,点Q在抛物线的对称轴上,是否存在以点B、C、P、Q为顶点的四边形是平行四边形?若存在,请求P点的坐标;若不存在,请说明理由.23. 在学习了矩形这节内容之后,明明同学发现生活中的很多矩形都很特殊,如我们的课本封面、A4 的打印纸等,这些矩形的长与宽之比都为 :1,我们将具有这类特征的矩形称为“完美矩形”如图(1),在“完美矩形”ABCD 中,点 P 为 AB 边上的定点,且 AP=AD.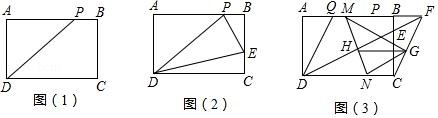 (1)、求证:PD=AB.(2)、如图(2),若在“完美矩形“ABCD 的边 BC 上有一动点 E,当 的值是多少时,△PDE 的周长最小?(3)、如图(3),点 Q 是边 AB 上的定点,且 BQ=BC.已知 AD=1,在(2)的条件下连接 DE 并延长交 AB 的延长线于点 F,连接 CF,G 为 CF 的中点,M、N 分别为线段 QF 和 CD 上的动点,且始终保持 QM=CN,MN 与 DF 相交于点 H,请问 GH 的长度是定值吗?若是,请求出它的值,若不是,请说明理由.
(1)、求证:PD=AB.(2)、如图(2),若在“完美矩形“ABCD 的边 BC 上有一动点 E,当 的值是多少时,△PDE 的周长最小?(3)、如图(3),点 Q 是边 AB 上的定点,且 BQ=BC.已知 AD=1,在(2)的条件下连接 DE 并延长交 AB 的延长线于点 F,连接 CF,G 为 CF 的中点,M、N 分别为线段 QF 和 CD 上的动点,且始终保持 QM=CN,MN 与 DF 相交于点 H,请问 GH 的长度是定值吗?若是,请求出它的值,若不是,请说明理由.