湖南省永州市新田县2017-2018学年九年级下学期数学期中考试试卷

试卷更新日期：2020-03-19 类型：期中考试

进入出卷网下载

一、单选题

1. 如图，数轴上两点A，B表示的数互为相反数，则点B表示的（）

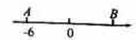A、-6 B、6 C、0 D、无法确定

查看试题解析
2. 下列运算正确是（）

A、 $a^{3} + a^{3} = a^{6}$ B、 $2 (a + 1) = 2 a + 1$ C、 ${(a b)}^{2} = a^{2} b^{2}$ D、 $a^{6} \div a^{3} = a^{2}$

查看试题解析
3. 下列交通标志中，是轴对称图形但不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 如图，AB∥CD，AD＝CD，∠1＝70°，则∠2的度数是（）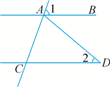

A、20° B、35° C、40° D、70°

查看试题解析
5. 实施新课改以来，某班学生经常采用“小组合作学习”的方式进行学习，值周班长小兵每周对各小组合作学习的情况进行综合评分，下表是其中一周的评分结果

“分值”这组数据的中位数和众数分别是（）

A、89，90 B、90，90 C、88，95 D、90，95

查看试题解析
6. 如图是一个正六棱柱的茶叶盒，其俯视图为（）

A、 B、 C、 D、

查看试题解析
7. 如图，△ABC的边AC与⊙O相交于C、D两点，且经过圆心O，边AB与⊙O相切，切点为B，已知∠A= $30^{°}$ ，则∠C的大小是（）

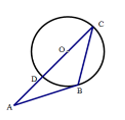A、60° B、45° C、30° D、15°

查看试题解析
8. 如图，在△ABC中，∠C＝90°，∠B＝30°，边AB的垂直平分线DE交AB于点E，交BC于点D.CD＝3，则BC的长为（）

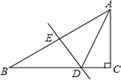A、6 B、9 C、6 $\sqrt{3}$ D、3 $\sqrt{3}$

查看试题解析
9. 如图所示的扇形是一个圆锥的侧面展开图，若∠AOB= $120 °$ ，弧AB的长为12 $π$ cm，则该圆锥的侧面积为（）

A、12 $π$ B、56 $π$ C、108 $π$ D、144 $π$

查看试题解析

二、填空题

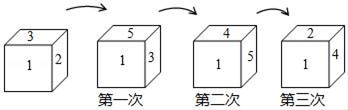
10. 有一个正六面体骰子放在桌面上，将骰子沿如图所示顺时针方向滚动，每滚动90°算一次，则滚动第2018次后，骰子朝下一面的数字是．

查看试题解析
11. 2011年3月，英国和新加坡研究人员制造出观测极限为0.00000005米的光学显微镜，其中0.00000005米用科学记数法表示为；

查看试题解析
12. 中国古代数学著作《算法统宗》中有这样一段记载：“三百七十八里关，初键步不为难，次日脚痛减一半，六朝才得到其关”其大意是：“有人要去某关口，路程378里，第一天键步行走，第二天起，由于脚痛，每天走的路程都为前一天的一半，一共走了六天才到达目的地，”则此人第六天走的路程为

查看试题解析
13. 若点P₁（﹣1，m），P₂（﹣2，n）在反比例函数 $y = \frac{k}{x}$ （ $k < 0$ ）的图象上，则mn．（填“＞”，“＜”或“=”）

查看试题解析
14. 如图所示，小明为了测量学校里一池塘的宽度AB，选取可以直达A，B两点的点O处，再分别取OA，OB的中点M，N，量得MN＝20m，则池塘的宽度AB为m.

查看试题解析
15. 不等式组 ${\begin{array}{l} - x + 4 < 2 \\ x - 3 \leq a \end{array}$ 的解集是 $2 < x \leq 4$ ，则a的值为

查看试题解析
16. 直线y₁＝k₁x＋b₁(k₁＞0)与y₂＝k₂x＋b₂(k₂＜0)相交于点(－2，0)，且两直线与y轴围成的三角形面积为4，那么b₁－b₂等于．

查看试题解析
17. 关于x的一元二次方程 $a x^{2} - 3 x - 1 = 0$ 的两个不相等的实数根都在-1和0之间（不包括-1和0），则a的取值范围是

查看试题解析
18. 取一个自然数，若它是奇数，则乘以3加上1，若它是偶数，则除以2，按此规则经过若干步的计算最终可得到1.这个结论在数学上还没有得到证明，但举例验证发现都是正确.例如：取自然数5，最少经过下面的5步运算可得1，如图：

请问，如果一个自然数m最少经过7步运算可得到1，则所有符合条件的m的值为

查看试题解析

三、解答题

19. 计算 $2^{2} - \sqrt[3]{125} + {(- 2018)}^{0} - {(- \frac{1}{4})}^{- 2} + 12 \cos 60 °$

查看试题解析
20. 先化简，再求值 $\frac{2 x}{x + 1} - \frac{2 x + 6}{x^{2} - 1} \div \frac{x + 3}{x^{2} - 2 x + 1}$ 其中 $x = \sqrt{2}$

查看试题解析
21. 为增强学生环保意识，某中学组织全校2000名学生参加环保知识大赛，比赛成绩均为整数，从中抽取部分同学的成绩进行统计，并绘制成如图统计图．请根据图中提供的信息，解答下列问题：

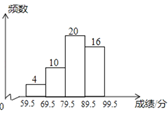(1)、若抽取的成绩用扇形图来描述，则表示“第三组（79.5～89.5）”的扇形的圆心角为多少度；

(2)、若成绩在90分以上（含90分）的同学可以获奖，请估计该校约有多少名同学获奖？

(3)、某班准备从成绩最好的4名同学（男、女各2名）中随机选取2名同学去社区进行环保宣传，则选出的同学恰好是1男1女的概率为多少．

查看试题解析
22. 某校开学初在家乐福超市购进A、B两种品牌的足球，购买A品牌足球花费了2500元，购买B品牌足球花费了2000元，且购买A品牌足球数量是购买B品牌足球数量的2倍．已知购买一个B品牌足球比购买一个A品牌足球多花30元．

(1)、购买一个A品牌、一个B品牌足球各需多少元？

(2)、该校响应习总书记“足球进校园”的号召，决定再次购进A、B两种品牌的足球共50个，恰逢家乐福超市对这两种品牌足球的售价进行调整，A品牌足球售价比第一次购买时提高了8%，B品牌足球按第一次购买时售价的9折出售，如果该校此次购买的总费用不超过3260元，那么，最多可以购买多少个B品牌足球？

查看试题解析
23. 如图，已知在四边形ABCD中，点E在AD上，∠BCE=∠ACD=90°，∠BAC=∠D ， BC=CE ．

(1)、求证：AC=CD；

(2)、若AC=AE ，求∠DEC的度数．

查看试题解析
24. 如图，在 $R t$ △ABC中，∠ACB= $90^{0}$ ，以点A为圆心，AC为半径，作⊙A，交AB于点D，交CA的延长线于点E，过点E作AB的平行线EF，交⊙A于点F，连接AF，BF，DF.

(1)、求证：BF是⊙A的切线；

(2)、当∠CAB等于多少度时，四边形ADFE为菱形？请给与证明.

(3)、若EF=1，AE=2，求cos∠CBA的值.

查看试题解析
25. 如图，在矩形ABCD中，点E是BC上的一个动点，过点E作EF⊥BD于点F，EG⊥AC于点G，CH⊥BD于点H，

(1)、试证明：CH=EF+EG

(2)、若点E在BC的延长线上，如图2，过点E作EF⊥BD于点F，EG⊥AC的延长线于点G，CH⊥BD于点H，则CH、EF、EG之间有怎样的数量关系，直接写出你的猜想；

(3)、如图3，BD是正方形ABCD的对角线，L在BD上，且BL=BC，连接CL，点E是CL上一点，EF⊥BD于点F，EG⊥BC于点G，猜想EF、EG、BD之间具有怎样的数量关系，直接写出你的猜想

查看试题解析
26. 如图，直线 $y = - \frac{2}{3} x + c$ 与x轴交于点A（3，0），与y轴交于点B，抛物线 $y = - \frac{4}{3} x^{2} + b x + c$ 经过点A，B.

(1)、求点B的坐标和抛物线的解析式；

(2)、M（m，0）为x轴上一个动点，过点M垂直于x轴的直线与直线AB和抛物线分别交于点P、N，
①点M在线段OA上运动，若以B，P，N为顶点的三角形与 $△ A P M$ 相似，求点M的坐标；

②点M在x轴上自由运动，若三个点M，P，N中恰有一点是其它两点所连线段的中点（三点重合除外），则称M，P，N三点为“共谐点”.请直接写出使得M，P，N三点成为“共谐点”的m的值.

查看试题解析