湖南省邵阳武冈市2018-2019学年九年级下学期数学期中考试试卷

试卷更新日期：2020-03-19 类型：期中考试

进入出卷网下载

一、单选题

1. 下列计算正确是 $($ 　　 $)$

A、 $a \cdot a^{2} = a^{3}$ B、(a³)²=a⁵ C、 $a + a^{2} = a^{3}$ D、 $a^{6} \div a^{2} = a^{3}$

查看试题解析
2. 下列实数中，为有理数的是（）

A、 $\sqrt{3}$ B、π C、 $\sqrt[3]{2}$ D、1

查看试题解析
3. 下列选项中最简分式是（）

A、 $\frac{1}{x^{2} + 1}$ B、 $\frac{2}{4 x^{2}}$ C、 $\frac{x + 1}{x^{2} - 1}$ D、 $\frac{3 x^{2} + x}{x}$

查看试题解析
4. 下列说法错误的是（）

A、必然事件的概率为1 B、数据1、2、2、3的平均数是2 C、连续掷一枚硬币，若5次都是正面朝上，则第六次仍然可能正面朝上 D、如果某种活动的中奖率为40%，那么参加这种活动10次必有4次中奖

查看试题解析
5. 如图，四边形ABCD是⊙O的内接四边形，若∠DAB=60°，则∠BCD的度数是（）

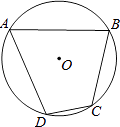A、60° B、90° C、100° D、120°

查看试题解析
6. 下列二次根式中，为最简二次根式的是 $($ $)$

A、 $\sqrt{45}$ B、 $\sqrt{x^{2} + y^{2}}$ C、 $\sqrt{\frac{b}{a}}$ D、 $\sqrt{1.7}$

查看试题解析
7. 在下列函数中，其图象与x轴没有交点的是（　　）

A、y=2x B、y=﹣3x+1 C、y=x² D、y= $\frac{1}{x}$

查看试题解析
8. 函数 $y = - x^{2} - 2 x + 3$ 的图象可以由 $y = - x^{2}$ 怎么平移得到？（）

A、先先右平移1个单位，再向上平移4个单位 B、先向左平移1个单位，再向下平移4个单位 C、先向左平移1个单位，再向上平移4个单位 D、先向右平移1个单位，再向下平移4个单位

查看试题解析
9. 关于 $x$ ， $y$ 的方程组 ${\begin{array}{l} 3 x + 2 y = 4 m + 5 \\ x - y = m - 1 \end{array}$ 的解满足 $2 x + 3 y > 7$ ，则 $m$ 的取值范围是（）

A、 $m < - \frac{1}{4}$ B、 $m < 0$ C、 $m > \frac{1}{3}$ D、 $m > 7$

查看试题解析
10. 如图，已知直线AB，CD被直线AC所截，AB∥CD，E是平面内任意一点（点E不在直线AB，CD，AC上），设∠BAE=α，∠DCE=β．下列各式：①α+β，②α﹣β，③β﹣α，④360°﹣α﹣β，∠AEC的度数可能是（）

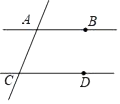A、①②③ B、①②④ C、①③④ D、①②③④

查看试题解析

二、填空题

11. ${(π - 3.14)}^{°} - \sqrt{4} =$

查看试题解析
12. 据报道.2018年5月1日到3日的五一劳动节期间，全国共接待游客1.34亿人次，旅游总收入达791.2亿元，用科学记数法表示数791.2亿元是元人民币.

查看试题解析
13. 当 $- 1 < a < 0$ 时，则 $\sqrt{{(a + \frac{1}{a})}^{2} - 4} - \sqrt{{(a - \frac{1}{a})}^{2} + 4} =$ .

查看试题解析
14. 若不等式组 ${\begin{matrix} 2 x - 3 \geq 0 \\ x \leq m \end{matrix}$ 无解，则m的取值范围是．

查看试题解析
15. 关于x的分式方程 $\frac{x + k}{x + 1}$ + $\frac{2 x}{x + 1}$ ＝1的解为非正数，则k的取值范围是．

查看试题解析
16. 如图，在四边形ABCD中， $AB / / CD$ ，AC、BD相交于点E，若 $\frac{AB}{CD} = \frac{1}{4}$ ，则 $\frac{AE}{AC} =$ ．

查看试题解析
17. 如图， $Rt △ A B C$ 中， $A B ⊥ B C$ ， $A B = 6$ ， $B C = 4$ ， $P$ 是 $△ A B C$ 内部的一个动点，且满足 $∠ P A B + ∠ P B A = 90^{°}$ ，则线段 $C P$ 长的最小值为.

查看试题解析
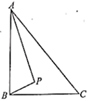18. 将正偶数按下表排列：

根据上面的规律，则2018所在行是第行．

查看试题解析

三、解答题

19. 计算：

(1)、 ${(- 2018)}^{0} - {(\frac{1}{2})}^{- 1} + \sqrt{9} - 2 \cos 60 °$

(2)、 $(1 + \frac{1}{x - 1}) \div \frac{x}{x^{2} - 1}$

查看试题解析
20. 解不等式组 ${\begin{matrix} 2 x - 3 < x ， ① \\ 3 (x - 1) - (x - 5) \geq 0 ， ② \end{matrix}$ ，并把它的解集在数轴上表示出来．

查看试题解析
21. 先化简，再求值： $(\frac{x^{2} - 2 x + 4}{x - 1} + 2 - x) \div \frac{x^{2} + 4 x + 4}{x - 1}$ ，其中 $x$ 满足 $x^{2} - 4 x + 3 = 0$ .

查看试题解析
22. 如图，在△ABC中，DE分别是AB，AC的中点，BE＝2DE，延长DE到点F，使得EF＝BE，连CF

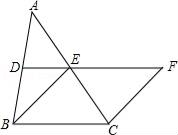(1)、求证：四边形BCFE是菱形；

(2)、若CE＝6，∠BEF＝120°，求菱形BCFE的面积．

查看试题解析
23. 一个圆锥的侧面展开图是半径为 $8 cm$ ，圆心角为120°的扇形，求：

(1)、圆锥的底面半径；

(2)、圆锥的全面积.

查看试题解析
24. 某中学艺术节期间，学校向学生征集书画作品，杨老师从全校30个班中随机抽取了4个班（用A，B，C，D表示），对征集到的作品的数量进行了分析统计，制作了两幅不完整的统计图．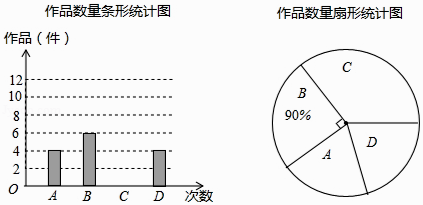
请根据以上信息，回答下列问题：

(1)、杨老师采用的调查方式是（填“普查”或“抽样调查”）；

(2)、请你将条形统计图补充完整，并估计全校共征集多少件作品？

(3)、如果全校征集的作品中有5件获得一等奖，其中有3名作者是男生，2名作者是女生，现要在获得一等奖的作者中选取两人参加表彰座谈会，请你用列表或树状图的方法，求恰好选取的两名学生性别相同的概率．

查看试题解析
25. 观察下列各式：① $f (1) = \frac{\sqrt{2} - 1}{2}$ ；② $f (2) = \frac{\sqrt{3} - \sqrt{2}}{2}$ ；③ $f (3) = \frac{2 - \sqrt{3}}{2}$ ；④ $f (4) = \frac{\sqrt{5} - 2}{2}$ …回答下列问题：

(1)、利用你观察到的规律直接写出f(n)=；

(2)、计算 $(2 \sqrt{2018} + 2) [f (1) + f (2) + f (3) + \dots + f (2017)]$ .

查看试题解析
26. 某校九年级数学小组在课外活动中，研究了同一坐标系中两个反比例函数 $y_{1} = \frac{k_{1}}{x}$ 与 $y_{2} = \frac{k_{2}}{x}$ $(k_{2} > k_{1} > 0)$ 在第一象限图象的性质，经历了如下探究过程：
操作猜想：

(1)、如图①，当 $k_{1} = 2$ ， $k_{2} = 6$ 时，在 $y$ 轴的正方向上取一点 $A$ 作 $x$ 轴的平行线交 $y_{1}$ 于点 $B$ ，交 $y_{2}$ 于点 $C$ .当 $O A = 1$ 时， $A B =$ ， $B C =$ ， $\frac{B C}{A B} =$ ；当 $O A = 3$ 时， $A B =$ ， $B C =$ ， $\frac{B C}{A B} =$ ；当 $O A = a$ 时，猜想 $\frac{B C}{A B} =$

(2)、在 $y$ 轴的正方向上任意取点 $A$ 作 $x$ 轴的平行线，交 $y_{1}$ 于点 $B$ 、交 $y_{2}$ 于点 $C$ ，请用含 $k_{1}$ 、 $k_{2}$ 的式子表示 $\frac{B C}{A B}$ 的值，并利用图②加以证明.

(3)、如图③，若 $k_{2} = 12$ ， $\frac{B C}{A B} = \frac{1}{2}$ ，在 $y$ 轴的正方向上分别取点 $A$ 、 $D$ $(O D > O A)$ 作 $x$ 轴的平行线，交 $y_{1}$ 于点 $B$ 、 $E$ ，交 $y_{2}$ 于点 $C$ 、 $F$ ，是否存在四边形 $A D F B$ 是正方形？如果存在，求 $O A$ 的长和点 $B$ 的坐标；如果不存在，请说明理由.

查看试题解析