人教版数学九年级上册第24章 24.1.1圆 同步练习
试卷更新日期：2017-08-25 类型：同步测试
一、单选题
-
1.
如图，四边形ABCD为矩形，AB=6，BC=8，连接AC，分别以A、C为圆心，以大于 长为半径画弧，两弧相交于点P、Q，连接PQ分别交AD、BC于点E、F，则EF的长为（ ）
A、 B、 C、8 D、102.如图，在平面直角坐标系中，⊙P的圆心是（2，a）（a＞2），半径为2，函数y=x的图象被⊙P截得的弦AB的长为 ，则a的值是（ ）
A、2 B、2+ C、2 D、2+3. 给出下列说法：①直径是弦；②优弧是半圆；③半径是圆的组成部分；④两个半径不相等的圆中，大的半圆的弧长小于小的半圆的周长．其中正确的有（ ）A、1个 B、2个 C、3个 D、4个4. 下列说法中正确的是（ ）A、弦是直径 B、弧是半圆 C、半圆是圆中最长的弧 D、直径是圆中最长的弦5. 下列语句中，不正确的有（ ）①直径是弦；
②弧是半圆；
③经过圆内一定点可以作无数条弦；
④长度相等的弧是等弧．
A、①③④ B、②③ C、② D、②④6. 下列说法错误的是（ ）A、圆有无数条直径 B、连接圆上任意两点之间的线段叫弦 C、过圆心的线段是直径 D、能够重合的圆叫做等圆7. 下列说法中，正确的是（ ）A、弦是直径 B、半圆是弧 C、过圆心的线段是直径 D、圆心相同半径相同的两个圆是同心圆8. 到圆心的距离不大于半径的点的集合是（ ）A、圆的外部 B、圆的内部 C、圆 D、圆的内部和圆9. 自行车车轮要做成圆形，实际上是根据圆的特征（ ）A、圆是轴对称图形 B、直径是圆中最长的弦 C、圆上各点到圆心的距离相等 D、圆是中心对称图形10. 下列语句正确的有（ ）①直径是弦；
②半圆是弧；
③长度相等的弧是等弧；
④经过圆内一定点可以作无数条弦；
⑤经过圆内一定点可以作无数条直径．
A、3 个 B、2个 C、1 个 D、4个11. 如图，△ABC中，BC＞AB＞AC．甲、乙两人想在BC上取一点P，使得∠APC=2∠ABC，其作法如下：（甲）作AB的中垂线，交BC于P点，则P即为所求
（乙）以B为圆心，AB长为半径画弧，交BC于P点，则P即为所求
对于两人的作法，下列判断何者正确？（ ）
A、两人皆正确 B、两人皆错误 C、甲正确，乙错误 D、甲错误，乙正确12.如图，MN是半径为1的⊙O的直径，点A在⊙O上，∠AMN=30°，点B为劣弧AN的中点．P是直径MN上一动点，则PA+PB的最小值为（ ）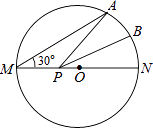
A、 B、1 C、2 D、2二、填空题
-
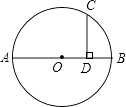
13. 如图，AB是⊙O的直径，点C在⊙O上，CD⊥AB，垂足为D，已知CD=4，OD=3，求AB的长是 ．
14. 已知线段AB=6cm，则经过A、B两点的最小的圆的半径为 ．15. 半径为5的⊙O中最大的弦长为 ．16. 如图，直线y= +3与坐标轴交于A、B两点，⊙O的半径为2，点P是⊙O上动点，△ABP面积的最大值为cm2 ．
17. 圆是中心对称图形，是它的对称中心．18. 线段AB=10cm，在以AB为直径的圆上，到点A的距离为5cm的点有个．19. 如图，小量角器的0°刻度线在大量角器的0°刻度线上，且小量角器的中心在大量角器的外缘边上．如果它们外缘边上的公共点P在大量角器上对应的度数为40°，那么在小量角器上对应的度数为 ． （只考虑小于90°的角度）
20. 我国魏晋时期数学家刘徽首创“割圆术”计算圆周率．随着时代发展，现在人们依据频率估计概率这一原理，常用随机模拟的方法对圆周率π进行估计，用计算机随机产生m个有序数对（x，y）（x，y是实数，且0≤x≤1，0≤y≤1），它们对应的点在平面直角坐标系中全部在某一个正方形的边界及其内部．如果统计出这些点中到原点的距离小于或等于1的点有n个，则据此可估计π的值为 ． （用含m，n的式子表示）三、解答题
-
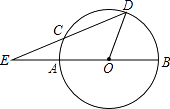
21. 如图，AB是半圆O的直径，D是半圆上的一点，∠DOB=75°，DC交BA的延长线于E，交半圆于C，且CE=AO，求∠E的度数．
22. 如图所示，AB为⊙O的直径，CD是⊙O的弦，AB、CD的延长线交于点E，已知AB=2DE，∠AEC=20°．求∠AOC的度数．
四、综合题
-
23. 已知线段MN=8，C是线段MN上一动点，在MN的同侧分别作等边△CMD和等边△CNE．(1)、
如图①，连接DN与EM，两条线段相交于点H，求证ME=DN，并求∠DHM的度数；
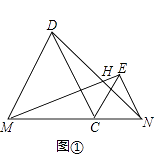(2)、如图②，过点D、E分别作线段MN的垂线，垂足分别为F、G，问：在点C运动过程中，DF+EG的长度是否为定值，如果是，请求出这个定值，如果不是请说明理由；
(3)、当点C由点M移到点N时，点H移到的路径长度为（直接写出结果）