湖南省益阳市南县2018-2019学年八年级下学期数学期中考试试卷
试卷更新日期：2020-03-19 类型：期中考试
一、单选题
-
1. 一个多边形的内角和是900°，这个多边形的边数是( )
A、4 B、5 C、6 D、72. 四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（ ）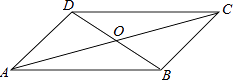
A、AB∥DC，AD∥BC B、AB=DC，AD=BC C、AO=CO，BO=DO D、AB∥DC，AD=BC3. 已知四边形ABCD是平行四边形，再从①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD四个条件中，选两个作为补充条件后，使得四边形ABCD是正方形，现有下列四种选法，其中错误的是（ ）A、选①② B、选②③ C、选①③ D、选②④4. 下列各组数据中，不能作为一个直角三角形三边长的一组是（ ）A、 B、 C、 D、5. 下列判断错误的是（ ）A、四个角相等的四边形是矩形 B、对角线垂直的四边形是菱形 C、对角线相等的平行四边形是矩形 D、对角线垂直的平行四边形是菱形6. 如图，已知∠AOB=60°，点P在边OA上，OP=12，点M，N在边OB上，PM=PN，若MN=2，则OM=（ ）
A、3 B、4 C、5 D、67. 如图，Rt△ABC中，AB=9，BC=6，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为（ ）
A、4 B、3 C、2 D、58. 如图，正方形OABC的两边OA、OC分别在x轴、y轴上，点D（5，3）在边AB上，以C为中心，把△CDB旋转90°，则旋转后点D的对应点D′的坐标是（ ）
A、（2，10） B、（﹣2，0） C、（2，10）或（﹣2，0） D、（10，2）或（﹣2，0）二、填空题
-
9. 如图，Rt△ABC中，∠ACB=90°，D为斜边AB的中点，AC=6cm，BC=8cm则CD的长为cm．
10. 如图，在Rt△ABC中，∠C=90°，D为AB的中点，DE⊥AC于点E．∠A=30°，AB=8，则DE的长度是 ．
11. 如图，Rt△ABC中，∠ACB=90°，BD是∠ABC的角平分线， AC=8， ，则D到AB的距离为 ．
12.将四根木条钉成的长方形木框变形为平行四边形ABCD的形状，并使其面积为长方形面积的一半（木条宽度忽略不计），则这个平行四边形的最小内角为度．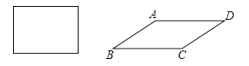
13. 如图，已知矩形ABCD，一条直线把矩形分割成两个多边形，若两个多边形的内角和分别为 和 ，则 的最小值为 ．
14.如图，正方形ABCD和正方形CEFG中，点D在CG上，BC=1，CE=3，H是AF的中点，那么CH的长是 ．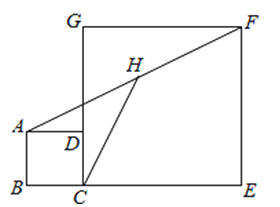
三、解答题
-
15. 在边长为1的小正方形网格中，△AOB的顶点均在格点上．
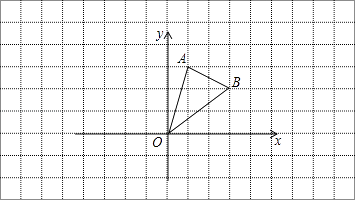(1)、B点关于y轴的对称点坐标为；(2)、将△AOB向左平移3个单位长度得到△A1O1B1 ， 请画出△A1O1B1；
(3)、在（2）的条件下，A1的坐标为 ．
16.如图，修公路遇到一座山，于是要修一条隧道．为了加快施工进度，想在小山的另一侧同时施工．为了使山的另一侧的开挖点C在AB的延长线上，设想过C点作直线AB的垂线L，过点B作一直线（在山的旁边经过），与L相交于D点，经测量∠ABD=135°，BD=800米，求直线L上距离D点多远的C处开挖？（≈1.414，精确到1米）
17. 已知：如图，在矩形ABCD中，点E，F分别在AB，CD边上，BE=DF，连接CE，AF．求证：AF=CE．
18. 如图，BD是△ABC的角平分线，点E、F分别在BC、AB上，且DE∥AB，EF∥AC，求证：BE=AF．
19. 勾股定理神秘而美妙，它的证法多样，其中的“面积法”给了李明灵感，他惊喜地发现；当两个全等的直角三角形如图（1）摆放时可以利用面积法”来证明勾股定理，过程如下
如图（1）∠DAB=90°，求证：a2+b2=c2
证明：连接DB，过点D作DF⊥BC交BC的延长线于点F，则DF=b-a
S四边形ADCB=
S四边形ADCB=
∴ 化简得：a2+b2=c2
请参照上述证法，利用“面积法”完成如图（2）的勾股定理的证明，如图（2）中∠DAB=90°，求证：a2+b2=c2
20. 如图，将矩形ABCD沿BD对折，点A落在E处，BE与CD相交于F，若AD=3，BD=6．
(1)、求证：△EDF≌△CBF；(2)、求∠EBC．
