湖南省浏阳市2018-2019学年八年级下学期数学期中考试试卷
试卷更新日期:2020-03-19 类型:期中考试
一、单选题
-
1. 若二次根式 有意义,则x的取值范围为( )A、x≥2 B、x≠2 C、x>2 D、x=22. 以下列各组数为三角形的三边,能构成直角三角形的是( )A、4,5,6 B、1,1, C、6,8,11 D、5,12,233. 下列计算错误的是 ( )A、 B、 C、 D、4. 在 ▱ ABCD中,∠A:∠B:∠C:∠D的度数比值可能是( )A、1:2:3:4 B、1:2:2:1 C、1:1:2:2 D、2:1:2:15. 估计×+的运算结果应在( )A、6到7之间 B、7到8之间 C、8到9之间 D、9到10之间6. 若平行四边形的一边长为10cm,则下列四组数据可以作为平行四边形的两条对角线的长度的是( )A、6cm 8cm B、8cm 12cm C、8cm 14cm D、6cm 14cm7. 如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=2,则AB=( )
 A、4 B、 C、 D、8. 若矩形的一条角平分线分一边为3cm和5cm两部分,则矩形的周长为( )A、22 B、26 C、22或26 D、28或269. 下列条件中不能确定四边形ABCD是平行四边形的是( )A、AB=CD,AD∥BC B、AB=CD,AB∥CD C、AB∥CD,AD∥BC D、AB=CD,AD=BC10. 把一个边长为1的正方形如图所示放在数轴上,以正方形的对角线为半径画弧交数轴于点A,则点A对应的数是( )
A、4 B、 C、 D、8. 若矩形的一条角平分线分一边为3cm和5cm两部分,则矩形的周长为( )A、22 B、26 C、22或26 D、28或269. 下列条件中不能确定四边形ABCD是平行四边形的是( )A、AB=CD,AD∥BC B、AB=CD,AB∥CD C、AB∥CD,AD∥BC D、AB=CD,AD=BC10. 把一个边长为1的正方形如图所示放在数轴上,以正方形的对角线为半径画弧交数轴于点A,则点A对应的数是( ) A、1 B、 C、 D、211. 实数a在数轴上的位置如图所示,则 + 化简后为( )
A、1 B、 C、 D、211. 实数a在数轴上的位置如图所示,则 + 化简后为( )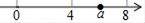 A、7 B、﹣7 C、2a﹣15 D、无法确定12. 如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD上的中点,P是线段BD上的一个动点,则PM+PN的最小值是( )
A、7 B、﹣7 C、2a﹣15 D、无法确定12. 如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD上的中点,P是线段BD上的一个动点,则PM+PN的最小值是( )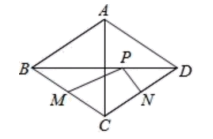 A、 B、3 C、 D、5
A、 B、3 C、 D、5二、填空题
-
13. 菱形的两条对角线的长为24和10,则菱形的边长是.14. 计算: , , .15. 若矩形的对角线长为2cm,两条对角线相交所成的一个夹角为60°,则该矩形的面积为
 . 16. 已知直角三角形的两边长分别为3、4.则第三边长为.17. 用50cm长的绳子围成一个平行四边形,使相邻两边的差为3cm,则较短的边长为cm.18. 由四个全等的直角三角形拼成如图所示的“赵爽弦图”,若直角三角形斜边长为2,最短的边长为1,则图中阴影部分的面积为 .
. 16. 已知直角三角形的两边长分别为3、4.则第三边长为.17. 用50cm长的绳子围成一个平行四边形,使相邻两边的差为3cm,则较短的边长为cm.18. 由四个全等的直角三角形拼成如图所示的“赵爽弦图”,若直角三角形斜边长为2,最短的边长为1,则图中阴影部分的面积为 .
三、解答题
-
19. 计算:(1)、(2)、20. 如图所示,在▱ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F,求证:BE=DF.
 21. 若a、b、c为△ABC的三边长,且a、b、c满足等式 ,求△ABC的面积.22. 小东拿着一根长竹竿进一个宽为3米的门,他先横着拿,进不去,又竖起来拿,结果竿比门高1米,当他把竿斜着时,两端刚好顶着门的对角,问:竹竿高多少米?23. 已知:如图,四边形ABCD中,AB⊥BC,AB=1,BC=2,CD=2,AD=3,求四边形ABCD的面积.
21. 若a、b、c为△ABC的三边长,且a、b、c满足等式 ,求△ABC的面积.22. 小东拿着一根长竹竿进一个宽为3米的门,他先横着拿,进不去,又竖起来拿,结果竿比门高1米,当他把竿斜着时,两端刚好顶着门的对角,问:竹竿高多少米?23. 已知:如图,四边形ABCD中,AB⊥BC,AB=1,BC=2,CD=2,AD=3,求四边形ABCD的面积. 24. 如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
24. 如图,△ABC中,AB=AC,AD是∠BAC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.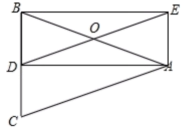 (1)、求证:四边形AEBD是矩形;(2)、当∠BAC=时,矩形AEBD是正方形.25. 在四边形ABCD中,已知AD//BC,∠ABC=90°.
(1)、求证:四边形AEBD是矩形;(2)、当∠BAC=时,矩形AEBD是正方形.25. 在四边形ABCD中,已知AD//BC,∠ABC=90°. (1)、若AC⊥BD,且AC=5,BD=3(如图1),求四边形ABCD的面积;(2)、若DE⊥BC于E,F是CD的中点,BD=BC,(如图2),求证:∠BAF=∠BCD.26. 已知:在△ABC年,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合).以AD为边作正方形ADEF,连接CF.
(1)、若AC⊥BD,且AC=5,BD=3(如图1),求四边形ABCD的面积;(2)、若DE⊥BC于E,F是CD的中点,BD=BC,(如图2),求证:∠BAF=∠BCD.26. 已知:在△ABC年,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合).以AD为边作正方形ADEF,连接CF. (1)、如图1,当点D在线段BC上时,求证:①BD⊥CF.
(1)、如图1,当点D在线段BC上时,求证:①BD⊥CF.② .
(2)、如图2,当点D在线段BC的延长线上时,其它条件不变,请直接写出CF、BC、CD三条线段之间的关系;(3)、如图3,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC的两侧,其它条件不变:①请直接写出CF、BC、CD三条线段之间的关系,
②若连接正方形对角线AE,DF,交点为0,连接OC,探究△AOC的形状,并说明理由.