湖南省邵阳市2018-2019学年八年级下学期数学期中考试试卷

试卷更新日期：2020-03-19 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各式： $\frac{a - b}{2}$ ， $\frac{x + 3}{x}$ ， $\frac{5 + y}{π}$ ， $\frac{a + b}{a - b}$ ， $\frac{1}{m}$ （x+y）中，是分式的共有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 计算3^﹣²的结果是（　　）

A、﹣9 B、﹣6 C、﹣ $\frac{1}{9}$ D、 $\frac{1}{9}$

查看试题解析
3. 如果分式 $\frac{x^{2} - 1}{2x + 2}$ 的值为0，则x的值是

A、1 B、0 C、－1 D、±1

查看试题解析
4. 以下列各组线段为边，能组成三角形的是（）

A、2cm，4cm，6cm B、8cm，6cm，4cm C、14cm，6cm，7cm D、2cm，3cm，6cm

查看试题解析
5. 有下列命题：①两点之间，线段最短； ②相等的角是对顶角； ③内错角互补，两直线平行．其中真命题的有（）

A、1个 B、2个 C、3个 D、0个

查看试题解析
6. 已知如图，△ABC为直角三角形，∠C＝90°，若沿图中虚线剪去∠C，则∠1+∠2等于（）

A、315° B、270° C、180° D、135°

查看试题解析
7. 等腰三角形的一个角是70°，则它的底角是（）

A、70° B、70°或55° C、80°和100° D、110°

查看试题解析
8. 如图，△ABC≌△BAD，点A和点B，点C和点D是对应点．如果∠D=70°，∠CAB=50°，那么∠DAB=（　　　　）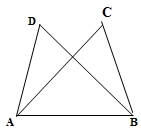

A、50° B、60° C、70° D、80°

查看试题解析
9. $A$ 、 $B$ 两地相距48千米，一艘轮船从 $A$ 地顺流航行至 $B$ 地，又立即从 $B$ 地逆流返回 $A$ 地，共用去9小时，已知水流速度为4千米/时，若设该轮船在静水中的速度为 $x$ 千米/时，则可列方程（）

A、 $\frac{48}{4 + x} + \frac{48}{4 - x} = 9$ B、 $\frac{96}{x + 4} + \frac{96}{x - 4} = 9$ C、 $\frac{48}{x} + 4 = 9$ D、 $\frac{48}{x + 4} + \frac{48}{x - 4} = 9$

查看试题解析
10. 已知 $a^{m} = 2$ ， $a^{n} = 3$ 则 $a^{4 m - 3 n}$ 的值是（）

A、 $- \frac{16}{27}$ B、 $\frac{16}{27}$ C、 $- \frac{27}{16}$ D、 $\frac{27}{16}$

查看试题解析

二、填空题

11. 当x＝时，分式 $\frac{3}{x - 2}$ 无意义．

查看试题解析
12. 如图，在△ABC中，AB的垂直平分线分别交AB，BC于点D，E，∠B=30°，∠BAC=80°，则∠CAE= ．

查看试题解析
13. 随着人们对环境的重视，新能源的开发迫在眉睫，石墨烯是现在世界上最薄的纳米材料，其理论厚度应是0.0000034m，用科学记数法表示是。

查看试题解析
14. 计算： $(x^{2} y - x y^{2}) \cdot \frac{x}{x^{2} - y^{2}}$ =。

查看试题解析
15. 已知AD是△ABC的中线，且AB=3cm，AC=6cm，BD=2cm，△ABC的周长为。

查看试题解析
16. 若分式方程 $1 + \frac{k}{x - 2} = \frac{1}{2 - x}$ 有增根，则 $k =$ 。

查看试题解析
17. 将“互为相反数的两个数之和等于0”写成如果，那么的形式．

查看试题解析
18. $△ A B C$ 中， $A B = A C = 12$ 厘米， $∠ B = ∠ C ， B C = 9$ 厘米，点D为AB的中点.如果点P在线段BC上以v厘米/秒的速度由B点向C点运动.同时，点Q在线段CA上由C点向A点运动.若点Q的运动速度为3厘米/秒，则当 $△ B P D$ 与 $△ C Q P$ 全等时，v的值为

查看试题解析

三、解答题

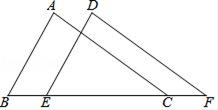
19. 先化简，再求值： $(\frac{3 x}{x - 2} - \frac{x}{x + 2}) \div \frac{x}{x^{2} - 4}$ ，在﹣2，0，1，2四个数中选一个合适的代入求值．

查看试题解析
20. 如图，已知AB∥DE ， AB＝DE ， BE＝CF ，求证：AC∥DF ．

查看试题解析
21. 如图，△ABC是等边三角形，BD是AC边上的高，延长BC至E，使CE=CD，连接DE。

(1)、求∠E的度数？

(2)、△DBE是什么三角形？为什么？

查看试题解析
22. 如图，在△ABC中，AB=CB，∠ABC=90°，D为AB延长线上一点，点E在BC边上，且BE=BD，连接AE、DE、DC．

(1)、求证：△ABE≌△CBD；

(2)、若∠CAE=30°，求∠BCD的度数．

查看试题解析
23. 在争创全国卫生城市的活动中，我县一青年突击队决定清运一重达50吨的垃圾，请根据以下信息，帮小刚计算青年突击队的实际清运速度。
信息一：清运开工后，由于附近居民主动参加义务劳动，清运速度比原计划提高了一倍。

信息二：结果比原计划提前了2小时完成任务。

查看试题解析
24. 根据下面图形，解答问题：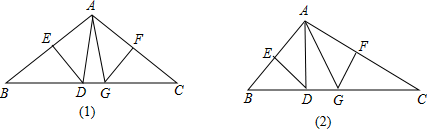

(1)、在△ABC中，AB=AC，∠BAC=100°，DE、FG分别是边AB、AC的垂直平分线（如图1），求∠DAG的度数？

(2)、在（1）中，若去掉“AB=AC”的条件，其余条件不变（如图2），还能求出∠DAG的度数吗？若能，请求出∠DAG的度数；若不能，请说明理由；

(3)、在（图2）的情况下试探索△ADG的周长与BC长的关系？

查看试题解析