人教版数学九年级上册第23章 23.1图形的旋转 同步练习
试卷更新日期:2017-08-24 类型:同步测试
一、单选题
-
1. 如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB延长线上,连接AD.下列结论一定正确的是( )
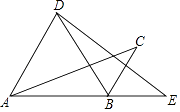 A、∠ABD=∠E B、∠CBE=∠C C、AD∥BC D、AD=BC2. 下列说法正确的是( )A、圆内接正六边形的边长与该圆的半径相等 B、在平面直角坐标系中,不同的坐标可以表示同一点 C、一元二次方程ax2+bx+c=0(a≠0)一定有实数根 D、将△ABC绕A点按顺时针方向旋转60°得△ADE,则△ABC与△ADE不全等3. 如图,将正方形ABCD中的阴影三角形绕点A顺时针旋转90°后,得到的图形为( )
A、∠ABD=∠E B、∠CBE=∠C C、AD∥BC D、AD=BC2. 下列说法正确的是( )A、圆内接正六边形的边长与该圆的半径相等 B、在平面直角坐标系中,不同的坐标可以表示同一点 C、一元二次方程ax2+bx+c=0(a≠0)一定有实数根 D、将△ABC绕A点按顺时针方向旋转60°得△ADE,则△ABC与△ADE不全等3. 如图,将正方形ABCD中的阴影三角形绕点A顺时针旋转90°后,得到的图形为( )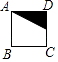 A、
A、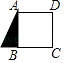 B、
B、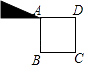 C、
C、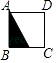 D、
D、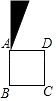 4. 如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是( )
4. 如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是( )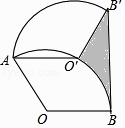 A、 B、2 ﹣ C、2 ﹣ D、4 ﹣5. 如图,在正方形ABCD中,点E,F分别在BC,CD上,且∠EAF=45°,将△ABE绕点A顺时针旋转90°,使点E落在点E'处,则下列判断不正确的是( )
A、 B、2 ﹣ C、2 ﹣ D、4 ﹣5. 如图,在正方形ABCD中,点E,F分别在BC,CD上,且∠EAF=45°,将△ABE绕点A顺时针旋转90°,使点E落在点E'处,则下列判断不正确的是( ) A、△AEE′是等腰直角三角形 B、AF垂直平分EE' C、△E′EC∽△AFD D、△AE′F是等腰三角形6. 如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( )
A、△AEE′是等腰直角三角形 B、AF垂直平分EE' C、△E′EC∽△AFD D、△AE′F是等腰三角形6. 如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( ) A、 B、2 C、3 D、27. 如图,网格纸上正方形小格的边长为1.图中线段AB和点P绕着同一个点做相同的旋转,分别得到线段A'B'和点P',则点P'所在的单位正方形区域是( )
A、 B、2 C、3 D、27. 如图,网格纸上正方形小格的边长为1.图中线段AB和点P绕着同一个点做相同的旋转,分别得到线段A'B'和点P',则点P'所在的单位正方形区域是( )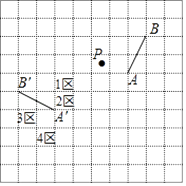 A、1区 B、2区 C、3区 D、4区8. 如图示,若△ABC内一点P满足∠PAC=∠PBA=∠PCB,则点P为△ABC的布洛卡点.三角形的布洛卡点(Brocard point)是法国数学家和数学教育家克洛尔(A.L.Crelle 1780﹣1855)于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡(Brocard 1845﹣1922)重新发现,并用他的名字命名.问题:已知在等腰直角三角形DEF中,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ=( )
A、1区 B、2区 C、3区 D、4区8. 如图示,若△ABC内一点P满足∠PAC=∠PBA=∠PCB,则点P为△ABC的布洛卡点.三角形的布洛卡点(Brocard point)是法国数学家和数学教育家克洛尔(A.L.Crelle 1780﹣1855)于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡(Brocard 1845﹣1922)重新发现,并用他的名字命名.问题:已知在等腰直角三角形DEF中,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ=( ) A、5 B、4 C、 D、9. 如图,大小不同的两个磁块,其截面都是等边三角形,小三角形边长是大三角形边长的一半,点O是小三角形的内心,现将小三角形沿着大三角形的边缘顺时针滚动,当由①位置滚动到④位置时,线段OA绕点O顺时针转过的角度是( )
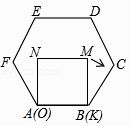
A、5 B、4 C、 D、9. 如图,大小不同的两个磁块,其截面都是等边三角形,小三角形边长是大三角形边长的一半,点O是小三角形的内心,现将小三角形沿着大三角形的边缘顺时针滚动,当由①位置滚动到④位置时,线段OA绕点O顺时针转过的角度是( ) A、240° B、360° C、480° D、540°10. 已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:
A、240° B、360° C、480° D、540°10. 已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示,按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转;…在这样连续6次旋转的过程中,点B,M间的距离可能是( )
 A、1.4 B、1.1 C、0.8 D、0.5
A、1.4 B、1.1 C、0.8 D、0.5二、填空题
-
11.
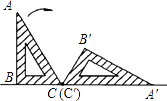
如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C′的位置,若BC=12cm,则顶点A从开始到结束所经过的路径长为 cm.
 12.
12.如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE⊥DG;③DE2+BG2=2a2+b2 , 其中正确结论是(填序号)
 13. 如图,在正方形ABCD中,AD=2 ,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为 .
13. 如图,在正方形ABCD中,AD=2 ,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为 . 14. 如图,点O是线段AB上一点,AB=4cm,AO=1cm,若线段AB绕点O顺时针旋转120°到线段A′B′的位置,则线段AB在旋转过程中扫过的图形的面积为
14. 如图,点O是线段AB上一点,AB=4cm,AO=1cm,若线段AB绕点O顺时针旋转120°到线段A′B′的位置,则线段AB在旋转过程中扫过的图形的面积为cm2 . (结果保留π)
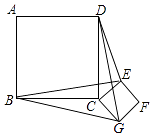
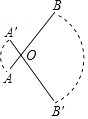 15. 如图,在△ABC中,∠ACB=90°,∠ABC=60°,AB=12cm,将△ABC以点B为中心顺时针旋转,使点C旋转到AB边延长线上的点D处,则AC边扫过的图形(阴影部分)的面积是cm2 . (结果保留π).
15. 如图,在△ABC中,∠ACB=90°,∠ABC=60°,AB=12cm,将△ABC以点B为中心顺时针旋转,使点C旋转到AB边延长线上的点D处,则AC边扫过的图形(阴影部分)的面积是cm2 . (结果保留π). 16. 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,将△ABC绕点C按顺时针方向旋转n度后,得到△EDC,此时,点D在AB边上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为 .
16. 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=2,将△ABC绕点C按顺时针方向旋转n度后,得到△EDC,此时,点D在AB边上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为 . 17. 如图,将矩形ABCD绕点C沿顺时针方向旋转90°到矩形A′B′CD′的位置,AB=2,AD=4,则阴影部分的面积为 .
17. 如图,将矩形ABCD绕点C沿顺时针方向旋转90°到矩形A′B′CD′的位置,AB=2,AD=4,则阴影部分的面积为 .
三、解答题
-
18.
在 的方格中,△ABC的三个顶点都在格点上.
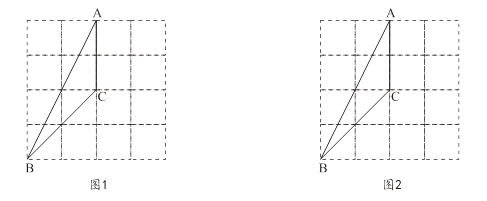 (1)、在图1中画出与△ABC成轴对称且与△ABC有公共边的格点三角形(画出一个即可);(2)、将图2中的△ABC绕着点C按顺时针方向旋转90°,画出经旋转后的三角形.
(1)、在图1中画出与△ABC成轴对称且与△ABC有公共边的格点三角形(画出一个即可);(2)、将图2中的△ABC绕着点C按顺时针方向旋转90°,画出经旋转后的三角形.四、综合题
-
19.
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为
A(﹣1,1),B(﹣3,1),C(﹣1,4).
①画出△ABC关于y轴对称的△A1B1C1;
②将△ABC绕着点B顺时针旋转90°后得到△A2BC2 , 请在图中画出△A2BC2 , 并求出线段BC旋转过程中所扫过的面积(结果保留π).
 20.
20.如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(﹣3,4),B(﹣5,2),C(﹣2,1).
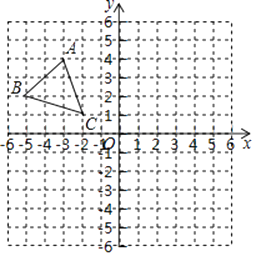 (1)、画出△ABC关于y轴对称图形△A1B1C1;(2)、画出将△ABC绕原点O逆时针方向旋转90°得到的△A2B2C2;(3)、求(2)中线段OA扫过的图形面积.21. 如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O逆时针旋转270°后得到扇形COD,AP,BQ分别切优弧 于点P,Q,且点P,Q在AB异侧,连接OP.
(1)、画出△ABC关于y轴对称图形△A1B1C1;(2)、画出将△ABC绕原点O逆时针方向旋转90°得到的△A2B2C2;(3)、求(2)中线段OA扫过的图形面积.21. 如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O逆时针旋转270°后得到扇形COD,AP,BQ分别切优弧 于点P,Q,且点P,Q在AB异侧,连接OP.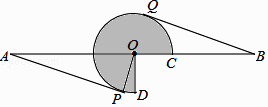 (1)、求证:AP=BQ;(2)、当BQ=4 时,求 的长(结果保留π);(3)、若△APO的外心在扇形COD的内部,求OC的取值范围.
(1)、求证:AP=BQ;(2)、当BQ=4 时,求 的长(结果保留π);(3)、若△APO的外心在扇形COD的内部,求OC的取值范围.
-