人教版数学九年级上册第22章 22.3实际问题与二次函数同步练习

试卷更新日期：2017-08-24 类型：同步测试

进入出卷网下载

一、解答题

1.
如图，某日的钱塘江观潮信息如表：
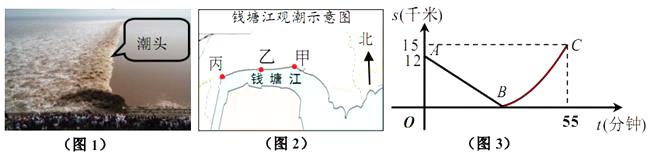
按上述信息，小红将“交叉潮”形成后潮头与乙地之间的距离 $s$ （千米）与时间 $t$ （分钟）的函数关系用图3表示，其中：“11：40时甲地‘交叉潮’的潮头离乙地12千米”记为点 $A (0 ， 12)$ ，点 $B$ 坐标为 $(m ， 0)$ ，曲线 $B C$ 可用二次函数 $s = \frac{1}{125} t^{2} + b t + c$ （ $b$ ， $c$ 是常数）刻画．

(1)、求 $m$ 的值，并求出潮头从甲地到乙地的速度；

(2)、11：59时，小红骑单车从乙地出发，沿江边公路以 $0.48$ 千米/分的速度往甲地方向去看潮，问她几分钟后与潮头相遇？

(3)、相遇后，小红立即调转车头，沿江边公路按潮头速度与潮头并行，但潮头过乙地后均匀加速，而单车最高速度为 $0.48$ 千米/分，小红逐渐落后，问小红与潮头相遇到落后潮头1.8千米共需多长时间？（潮水加速阶段速度 $v = v_{0} + \frac{2}{125} (t - 30)$ ， $v_{0}$ 是加速前的速度）．

查看试题解析
2.
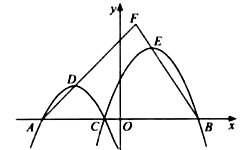如图，在平面直角坐标系 $x Ο y$ 中，已知 $Α$ ， $Β$ 两点的坐标分别为 $(- 4 ， 0)$ ， $(4 ， 0)$ ， $C (m ， 0)$ 是线段 $Α Β$ 上一点（与 $Α$ ， $Β$ 点不重合），抛物线 $L_{1} ：$ $y = a x^{2} + b_{1} x + c_{1}$ （ $a < 0$ ）经过点 $Α$ ， $C$ ，顶点为 $D$ ，抛物线 $L_{2} ：$ $y = a x^{2} + b_{2} x + c_{2}$ （ $a < 0$ ）经过点 $C$ ， $Β$ ，顶点为 $Ε$ ， $Α D$ ， $Β Ε$ 的延长线相交于点 $F$ ．

(1)、若 $a = - \frac{1}{2}$ ， $m = - 1$ ，求抛物线 $L_{1}$ ， $L_{2}$ 的解析式；

(2)、若 $a = - 1$ ， $Α F ⊥ Β F$ ，求 $m$ 的值；

(3)、是否存在这样的实数 $a$ （ $a < 0$ ），无论 $m$ 取何值，直线 $Α F$ 与 $Β F$ 都不可能互相垂直？若存在，请直接写出 $a$ 的两个不同的值；若不存在，请说明理由．

查看试题解析

二、综合题

3. 某超市销售一种牛奶，进价为每箱24元，规定售价不低于进价．现在的售价为每箱36元，每月可销售60箱．市场调查发现：若这种牛奶的售价每降价1元，则每月的销量将增加10箱，设每箱牛奶降价x元（x为正整数），每月的销量为y箱．

(1)、写出y与x中间的函数关系书和自变量x的取值范围；

(2)、超市如何定价，才能使每月销售牛奶的利润最大？最大利润是多少元？

查看试题解析
4. 青岛市某大酒店豪华间实行淡季、旺季两种价格标准，旺季每间价格比淡季上涨 $\frac{1}{3}$ ．下表是去年该酒店豪华间某两天的相关记录：

淡季
旺季
未入住房间数
10
0
日总收入（元）
24000
40000

(1)、该酒店豪华间有多少间？旺季每间价格为多少元？

(2)、今年旺季来临，豪华间的间数不变．经市场调查发现，如果豪华间仍旧实行去年旺季价格，那么每天都客满；如果价格继续上涨，那么每增加25元，每天未入住房间数增加1间．不考虑其他因素，该酒店将豪华间的价格上涨多少元时，豪华间的日总收入最高？最高日总收入是多少元？

查看试题解析
5. 农经公司以30元/千克的价格收购一批农产品进行销售，为了得到日销售量p（千克）与销售价格x（元/千克）之间的关系，经过市场调查获得部分数据如下表：
销售价格x（元/千克）
30
35
40
45
50
日销售量p（千克）
600
450
300
150
0

(1)、请你根据表中的数据，用所学过的一次函数、二次函数、反比例函数的知识确定p与x之间的函数表达式；

(2)、农经公司应该如何确定这批农产品的销售价格，才能使日销售利润最大？

(3)、若农经公司每销售1千克这种农产品需支出a元（a＞0）的相关费用，当40≤x≤45时，农经公司的日获利的最大值为2430元，求a的值．（日获利=日销售利润﹣日支出费用）

查看试题解析
6.
如图，二次函数y=ax²+bx+c（a≠0）的图象交x轴于A、B两点，交y轴于点D，点B的坐标为（3，0），顶点C的坐标为（1，4）．

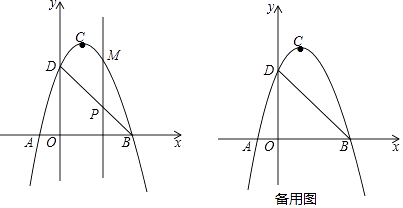(1)、求二次函数的解析式和直线BD的解析式；

(2)、点P是直线BD上的一个动点，过点P作x轴的垂线，交抛物线于点M，当点P在第一象限时，求线段PM长度的最大值；

(3)、在抛物线上是否存在异于B、D的点Q，使△BDQ中BD边上的高为2 $\sqrt{2}$ ？若存在求出点Q的坐标；若不存在请说明理由．

查看试题解析
7.
如图，抛物线y=﹣（x﹣1）²+c与x轴交于A，B（A，B分别在y轴的左右两侧）两点，与y轴的正半轴交于点C，顶点为D，已知A（﹣1，0）．

(1)、求点B，C的坐标；

(2)、判断△CDB的形状并说明理由；

(3)、将△COB沿x轴向右平移t个单位长度（0＜t＜3）得到△QPE．△QPE与△CDB重叠部分（如图中阴影部分）面积为S，求S与t的函数关系式，并写出自变量t的取值范围．

查看试题解析
8. 某厂按用户的月需求量x（件）完成一种产品的生产，其中x＞0，每件的售价为18万元，每件的成本y（万元）是基础价与浮动价的和，其中基础价保持不变，浮动价与月需求量x（件）成反比，经市场调研发现，月需求量x与月份n（n为整数，1≤n≤12），符合关系式x=2n²﹣2kn+9（k+3）（k为常数），且得到了表中的数据．
月份n（月）
1
2
成本y（万元/件）
11
12
需求量x（件/月）
120
100

(1)、求y与x满足的关系式，请说明一件产品的利润能否是12万元；

(2)、求k，并推断是否存在某个月既无盈利也不亏损；

(3)、在这一年12个月中，若第m个月和第（m+1）个月的利润相差最大，求m．

查看试题解析
9. 小明同学在一次社会实践活动中，通过对某种蔬菜在1月份至7月份的市场行情进行统计分析后得出如下规律：
①该蔬菜的销售价P（单位：元/千克）与时间x（单位：月份）满足关系：P=9﹣x
②该蔬菜的平均成本y（单位：元/千克）与时间x（单位：月份）满足二次函数关系y=ax²+bx+10，已知4月份的平均成本为2元/千克，6月份的平均成本为1元/千克．

(1)、求该二次函数的解析式；

(2)、请运用小明统计的结论，求出该蔬菜在第几月份的平均利润L（单位：元/千克）最大？最大平均利润是多少？（注：平均利润=销售价﹣平均成本）

查看试题解析
10. 夏季空调销售供不应求，某空调厂接到一份紧急订单，要求在10天内（含10天）完成任务，为提高生产效率，工厂加班加点，接到任务的第一天就生产了空调42台，以后每天生产的空调都比前一天多2台，由于机器损耗等原因，当日生产的空调数量达到50台后，每多生产一台，当天生产的所有空调，平均每台成本就增加20元．

(1)、设第x天生产空调y台，直接写出y与x之间的函数解析式，并写出自变量x的取值范围．

(2)、若每台空调的成本价（日生产量不超过50台时）为2000元，订购价格为每台2920元，设第x天的利润为W元，试求W与x之间的函数解析式，并求工厂哪一天获得的利润最大，最大利润是多少．

查看试题解析

	淡季	旺季
未入住房间数	10	0
日总收入（元）	24000	40000

销售价格x（元/千克）	30	35	40	45	50
日销售量p（千克）	600	450	300	150	0

月份n（月）	1	2
成本y（万元/件）	11	12
需求量x（件/月）	120	100

人教版数学九年级上册第22章 22.3实际问题与二次函数 同步练习

一、解答题

二、综合题

人教版数学九年级上册第22章 22.3实际问题与二次函数同步练习