人教版数学九年级上册第22章 22.2用函数观点看一元二次方程同步练习

试卷更新日期：2017-08-24 类型：同步测试

进入出卷网下载

一、单选题

1. 观察下列表格，求一元二次方程x²﹣x=1.1的一个近似解是（　　）
       x
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
   x²﹣x
0.11
0.24
0.39
0.56
0.75
0.96
1.19
1.44
1.71

A、0.11 B、1.6 C、1.7   D、1.19

查看试题解析

2. 已知二次函数y=ax²+bx+c的y与x的部分对应值如下表：

x	…	﹣1	0	1	3	…
y	…	﹣3	1	3	1	…

则方程ax²+bx+c=0的正根介于（　　）

A、3与4之间 B、2与3之间 C、1与2之间 D、0与1之间

查看试题解析

3. 已知关于x的方程 $x^{2} + 1 = \frac{k}{x}$ 有一个正的实数根，则k的取值范围是（　　）

A、k＜0 B、k＞0 C、k≤0 D、k≥0

查看试题解析
4.
小颖用计算器探索方程ax²+bx+c=0的根，作出如图所示的图象，并求得一个近似根x=﹣3.4，则方程的另一个近似根（精确到0.1）为（　　）

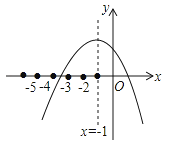A、4.4 B、3.4 C、2.4 D、1.4

查看试题解析
5. 已知二次函数y=x²+2x﹣k，小聪利用计算器列出了下表：
         x
   ﹣4.1
     ﹣4.2
   ﹣4.3
    ﹣4.4
x²+2x﹣k
   ﹣1.39
     ﹣0.76
   ﹣0.11
      0.56
那么方程x²+2x﹣k=0的一个近似根是（　　）

A、﹣4.1    B、﹣4.2 C、4.3 D、﹣4.4

查看试题解析
6. 根据下列表格的对应值，判断方程ax²+bx+c=0（a≠0，a、b、c为常数）一个解的范围是（　　）
x
3.23
3.24
3.25
3.26
ax²+bx+c
﹣0.06
﹣0.02
0.03
0.09

A、3＜x＜3.23 B、3.23＜x＜3.24 C、3.24＜x＜3.25 D、3.25＜x＜3.26

查看试题解析
7. 已知二次函数y=ax²+bx+c中，函数y与自变量x的部分对应值如表，则方程ax²+bx+c=0的一个解的范围是（）
x
6.17
6.18
6.19
6.20
y
﹣0.03
﹣0.01
0.02
0.04

A、﹣0.01＜x＜0.02 B、6.17＜x＜6.18 C、6.18＜x＜6.19 D、6.19＜x＜6.20

查看试题解析
8. 下列表格是二次函数y=ax²+bx+c（d≠0）的自变量x与函数y的一些对应值，由此可以判断方程ax²+bx+c=0（a≠0）的一个根在（）
x
6.17
6.18
6.19
6.20
y=ax²+bx+c
﹣0.03
﹣0.01
0.02
0.06

A、﹣0.01﹣0.02之间 B、0.02﹣0.06之间 C、6.17﹣6.18之间 D、6.18﹣6.19之间

查看试题解析
9.
如图，已知二次函数y=ax²+bx+c的部分图象，由图象可知关于x的一元二次方程ax²+bx+c=0的两个根分别是x₁=1.6，x₂=（　　）

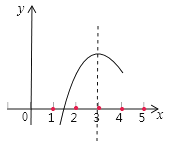A、﹣1.6 B、3.2 C、4.4 D、以上都不对

查看试题解析
10. 下表是一组二次函数y=x²+3x﹣5的自变量x与函数值y的对应值：
x
1
1.1
1.2
1.3
1.4
y
﹣1
﹣0.49
0.04
0.59
1.16
那么方程x²+3x﹣5=0的一个近似根是（）

A、1 B、1.1 C、1.2 D、1.3

查看试题解析

二、填空题

11. 方程2x²﹣4x=5的近似根是．

查看试题解析
12. 我们把一元二次方程x²﹣2x﹣3=0的解看成是抛物线y=x²﹣2x﹣3与x轴的交点的横坐标，如果把方程x²﹣2x﹣3=0适当地变形，那么方程的解还可以看成是函数与函数的图象交点的横坐标（写出其中的一对）．

查看试题解析
13. 小亮同学在探究一元二次方程ax²+bx+c=0的近似解时，填好了下面的表格：
x
3.23
3.24
3.25
3.26
ax²+bx+c
﹣0.06
﹣0.02
0.03
0.09
根据以上信息请你确定方程ax²+bx+c=0的一个解的范围是　　．

查看试题解析
14. 根据下列表中的对应值：
x
2.1
2.2
2.3
2.4
ax²+bx+c
﹣1.39
﹣0.76
﹣0.11
0.56
判断方程ax²+bx+c=0（a≠0，a，b，c为常数）的一个解的取值范围为．

查看试题解析
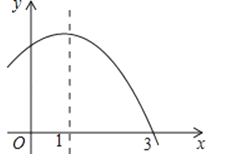
15. 在平面直角坐标系中，抛物线y=ax²+bx+c（a，b，c是常数，a＞0）的部分图象如图所示，直线x=1是它的对称轴．若一元二次方程ax²+bx+c=0的一个根x₁的取值范围是2＜x₁＜3，则它的另一个根x₂的取值范围是．

查看试题解析

三、解答题

16. 利用函数图象求2x²﹣x﹣3=0的解

查看试题解析
17. 请画出适当的函数图象，求方程x²= $\frac{1}{2}$ x+3的解

查看试题解析
18. 画图求方程x²=﹣x+2的解，你是如何解决的呢？我们来看一看下面两位同学不同的方法．
甲：先将方程x²=﹣x+2化为x²+x﹣2=0，再画出y=x²+x﹣2的图象，观察它与x轴的交点，得出方程的解；
乙：分别画出函数y=x²和y=﹣x+2的图象，观察它们的交点，并把交点的横坐标作为方程的解．
你对这两种解法有什么看法？请与你的同学交流．

查看试题解析
19.
已知二次函数y=﹣x²+2x+m的部分图象如图所示，你能确定关于x的一元二次方程﹣x²+2x+m=0的解？

查看试题解析

x	1.1	1.2	1.3	1.4	1.5	1.6	1.7	1.8	1.9
x²﹣x	0.11	0.24	0.39	0.56	0.75	0.96	1.19	1.44	1.71

x	﹣4.1	﹣4.2	﹣4.3	﹣4.4
x²+2x﹣k	﹣1.39	﹣0.76	﹣0.11	0.56

x	3.23	3.24	3.25	3.26
ax²+bx+c	﹣0.06	﹣0.02	0.03	0.09

x	6.17	6.18	6.19	6.20
y	﹣0.03	﹣0.01	0.02	0.04

x	6.17	6.18	6.19	6.20
y=ax²+bx+c	﹣0.03	﹣0.01	0.02	0.06

x	3.23	3.24	3.25	3.26
ax²+bx+c	﹣0.06	﹣0.02	0.03	0.09

人教版数学九年级上册第22章 22.2用函数观点看一元二次方程 同步练习

一、单选题

二、填空题

三、解答题

人教版数学九年级上册第22章 22.2用函数观点看一元二次方程同步练习