人教版数学九年级上册第22章 22.1.3二次函数y=ax2+bx+c的图像和性质 同步练习
试卷更新日期:2017-08-24 类型:同步测试
一、单选题
-
1. 抛物线 (m是常数)的顶点在 ( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. a≠0,函数y= 与y=﹣ax2+a在同一直角坐标系中的大致图象可能是( )A、
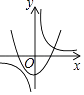 B、
B、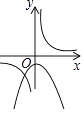 C、
C、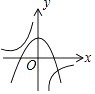 D、
D、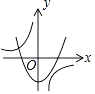 3. 抛物线y=﹣ (x+ )2﹣3的顶点坐标是( )A、( ,﹣3) B、(﹣ ,﹣3) C、( ,3) D、(﹣ ,3)4. 矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,这个点与点A重合,此时抛物线的函数表达式为y=x2 , 再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为( )
3. 抛物线y=﹣ (x+ )2﹣3的顶点坐标是( )A、( ,﹣3) B、(﹣ ,﹣3) C、( ,3) D、(﹣ ,3)4. 矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,这个点与点A重合,此时抛物线的函数表达式为y=x2 , 再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为( )
A、y=x2+8x+14 B、y=x2-8x+14 C、y=x2+4x+3 D、y=x2-4x+35. 函数y=﹣21(x﹣2)2+5的顶点坐标为( )A、(2,5) B、(﹣2,5) C、(2,﹣5) D、(﹣2,-5)6. 对于二次函数y=x2﹣2mx﹣3,下列结论错误的是( )A、它的图象与x轴有两个交点 B、方程x2﹣2mx=3的两根之积为﹣3 C、它的图象的对称轴在y轴的右侧 D、x<m时,y随x的增大而减小7. 抛物线y=2(x﹣3)2+4顶点坐标是( )A、(3,4) B、(﹣3,4) C、(3,﹣4) D、(2,4)8. 对于函数y=﹣2(x﹣m)2的图象,下列说法不正确的是( )A、开口向下 B、对称轴是x=m C、最大值为0 D、与y轴不相交9. 抛物线y=x2﹣2x+3 的对称轴为( )A、直线x=﹣1 B、直线x=﹣2 C、直线x=1 D、直线x=210. 二次函数y=x2+2x﹣3的顶点坐标是( )A、(﹣1,﹣3) B、(1,﹣4) C、(﹣1,﹣2) D、(﹣1,﹣4)11. 抛物线y=3(x﹣5)2的顶点坐标是( )A、(5,0) B、(3,5) C、(-3,5) D、(﹣5,0)12. 由于被墨水污染,一道数学题仅能见到如下文字:已知二次函数y=ax2+bx+c的图象过点(1,0)…求证:这个二次函数的图象关于直线x=2对称,根据现有信息,题中的二次函数具有的性质:
(1 )过点(3,0)
(2 )顶点是(1,﹣2)
(3 )在x轴上截得的线段的长度是2
(4 )c=3a
正确的个数( )
A、4个 B、3个 C、2个 D、1个二、填空题
-
13. 当x=时,二次函数y=x2﹣2x+6有最小值 .14. 经过A(4,0),B(﹣2,0),C(0,3)三点的抛物线解析式是 .15. 已知一个二次函数的图象开口向上,顶点坐标为(0,﹣1 ),那么这个二次函数的解析式可以是 . (只需写一个)16. 对于实数p,q,我们用符号min{p,q}表示p,q两数中较小的数,如min{1,2}=1,因此,min{﹣ ,﹣ }=;若min{(x﹣1)2 , x2}=1,则x= .
17. 如图,在边长为6cm的正方形ABCD中,点E、F、G、H分别从点A、B、C、D同时出发,均以1cm/s的速度向点B、C、D、A匀速运动,当点E到达点B时,四个点同时停止运动,在运动过程中,当运动时间为 s时,四边形EFGH的面积最小,其最小值是 cm2 .
三、解答题
-
18. 已知抛物线的顶点为(﹣1,2),且过 点(2,1),求该抛物线的函数解析式.19. 已知当x=2时,二次函数有最大值8,且图象过点(0,4),求此函数的关系式.
四、综合题
-
20. 在平面直角坐标系xOy中,抛物线y=ax2+bx+2过点A(﹣2,0),B(2,2),与y轴交于点C.
 (1)、求抛物线y=ax2+bx+2的函数表达式;(2)、若点D在抛物线y=ax2+bx+2的对称轴上,求△ACD的周长的最小值;(3)、在抛物线y=ax2+bx+2的对称轴上是否存在点P,使△ACP是直角三角形?若存在直接写出点P的坐标,若不存在,请说明理由.21. 如图1,抛物线y=ax2+bx+2与x轴交于A,B两点,与y轴交于点C,AB=4,矩形OBDC的边CD=1,延长DC交抛物线于点E.
(1)、求抛物线y=ax2+bx+2的函数表达式;(2)、若点D在抛物线y=ax2+bx+2的对称轴上,求△ACD的周长的最小值;(3)、在抛物线y=ax2+bx+2的对称轴上是否存在点P,使△ACP是直角三角形?若存在直接写出点P的坐标,若不存在,请说明理由.21. 如图1,抛物线y=ax2+bx+2与x轴交于A,B两点,与y轴交于点C,AB=4,矩形OBDC的边CD=1,延长DC交抛物线于点E.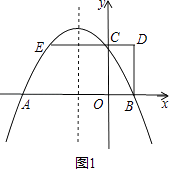 (1)、求抛物线的解析式;(2)、如图2,点P是直线EO上方抛物线上的一个动点,过点P作y轴的平行线交直线EO于点G,作PH⊥EO,垂足为H.设PH的长为l,点P的横坐标为m,求l与m的函数关系式(不必写出m的取值范围),并求出l的最大值;
(1)、求抛物线的解析式;(2)、如图2,点P是直线EO上方抛物线上的一个动点,过点P作y轴的平行线交直线EO于点G,作PH⊥EO,垂足为H.设PH的长为l,点P的横坐标为m,求l与m的函数关系式(不必写出m的取值范围),并求出l的最大值;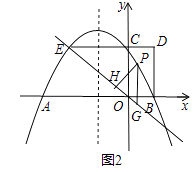 (3)、如果点N是抛物线对称轴上的一点,抛物线上是否存在点M,使得以M,A,C,N为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的点M的坐标;若不存在,请说明理由.
(3)、如果点N是抛物线对称轴上的一点,抛物线上是否存在点M,使得以M,A,C,N为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的点M的坐标;若不存在,请说明理由.