人教版数学九年级上册第22章 22.1.3二次函数y=a(x-h)2+k的图像和性质 同步练习
试卷更新日期:2017-08-24 类型:同步测试
一、单选题
-
1. 矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,这个点与点A重合,此时抛物线的函数表达式为y=x2 , 再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为( )
A、y=x2+8x+14 B、y=x2-8x+14 C、y=x2+4x+3 D、y=x2-4x+32. 抛物线 (m是常数)的顶点在 ( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. a≠0,函数y= 与y=﹣ax2+a在同一直角坐标系中的大致图象可能是( )A、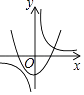 B、
B、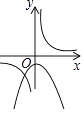 C、
C、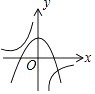 D、
D、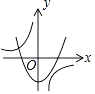 4. 抛物线y=﹣ (x+ )2﹣3的顶点坐标是( )A、( ,﹣3) B、(﹣ ,﹣3) C、( ,3) D、(﹣ ,3)5. 将抛物线y=2(x﹣4)2﹣1先向左平移4个单位长度,再向上平移2个单位长度,平移后所得抛物线的解析式为( )A、y=2x2+1 B、y=2x2﹣3 C、y=2(x﹣8)2+1 D、y=2(x﹣8)2﹣36. 对于二次函数y=x2﹣2mx﹣3,下列结论错误的是( )A、它的图象与x轴有两个交点 B、方程x2﹣2mx=3的两根之积为﹣3 C、它的图象的对称轴在y轴的右侧 D、x<m时,y随x的增大而减小7. 将抛物线y=2x2向右平移3个单位,再向下平移5个单位,得到的抛物线的表达式为( )A、y=2(x﹣3)2﹣5 B、y=2(x+3)2+5 C、y=2(x﹣3)2+5 D、y=2(x+3)2﹣58. 抛物线y=2(x﹣3)2+4顶点坐标是( )A、(3,4) B、(﹣3,4) C、(3,﹣4) D、(2,4)9. 对于函数y=﹣2(x﹣m)2的图象,下列说法不正确的是( )A、开口向下 B、对称轴是x=m C、最大值为0 D、与y轴不相交10. 二次函数y=2x2+4x﹣3的图象的顶点坐标是( )A、(0,﹣3) B、(1,3) C、(﹣1,﹣3) D、(﹣1,﹣5)11. 抛物线y=3(x﹣1)2+2的顶点坐标是( )A、(1,﹣2) B、(﹣1,2) C、(1,2) D、(﹣1,﹣2)12. 若抛物线y=(m﹣1)x 开口向下,则m的取值是( )A、﹣1或2 B、1或﹣2 C、2 D、﹣1
4. 抛物线y=﹣ (x+ )2﹣3的顶点坐标是( )A、( ,﹣3) B、(﹣ ,﹣3) C、( ,3) D、(﹣ ,3)5. 将抛物线y=2(x﹣4)2﹣1先向左平移4个单位长度,再向上平移2个单位长度,平移后所得抛物线的解析式为( )A、y=2x2+1 B、y=2x2﹣3 C、y=2(x﹣8)2+1 D、y=2(x﹣8)2﹣36. 对于二次函数y=x2﹣2mx﹣3,下列结论错误的是( )A、它的图象与x轴有两个交点 B、方程x2﹣2mx=3的两根之积为﹣3 C、它的图象的对称轴在y轴的右侧 D、x<m时,y随x的增大而减小7. 将抛物线y=2x2向右平移3个单位,再向下平移5个单位,得到的抛物线的表达式为( )A、y=2(x﹣3)2﹣5 B、y=2(x+3)2+5 C、y=2(x﹣3)2+5 D、y=2(x+3)2﹣58. 抛物线y=2(x﹣3)2+4顶点坐标是( )A、(3,4) B、(﹣3,4) C、(3,﹣4) D、(2,4)9. 对于函数y=﹣2(x﹣m)2的图象,下列说法不正确的是( )A、开口向下 B、对称轴是x=m C、最大值为0 D、与y轴不相交10. 二次函数y=2x2+4x﹣3的图象的顶点坐标是( )A、(0,﹣3) B、(1,3) C、(﹣1,﹣3) D、(﹣1,﹣5)11. 抛物线y=3(x﹣1)2+2的顶点坐标是( )A、(1,﹣2) B、(﹣1,2) C、(1,2) D、(﹣1,﹣2)12. 若抛物线y=(m﹣1)x 开口向下,则m的取值是( )A、﹣1或2 B、1或﹣2 C、2 D、﹣1二、填空题
-
13. 当x=时,二次函数y=x2﹣2x+6有最小值 .14. 如果抛物线y=ax2﹣3的顶点是它的最低点,那么a的取值范围是 .15. 抛物线y=﹣ax2+2ax+3(a≠0)的对称轴是 .16. 对于实数p,q,我们用符号min{p,q}表示p,q两数中较小的数,如min{1,2}=1,因此,min{﹣ ,﹣ }=;若min{(x﹣1)2 , x2}=1,则x= .
17. 如图,若抛物线y=ax2+bx+c上的P(4,0),Q两点关于它的对称轴x=1对称,则Q点的坐标为 . 18. 如图,在边长为6cm的正方形ABCD中,点E、F、G、H分别从点A、B、C、D同时出发,均以1cm/s的速度向点B、C、D、A匀速运动,当点E到达点B时,四个点同时停止运动,在运动过程中,当运动时间为 s时,四边形EFGH的面积最小,其最小值是 cm2 .
18. 如图,在边长为6cm的正方形ABCD中,点E、F、G、H分别从点A、B、C、D同时出发,均以1cm/s的速度向点B、C、D、A匀速运动,当点E到达点B时,四个点同时停止运动,在运动过程中,当运动时间为 s时,四边形EFGH的面积最小,其最小值是 cm2 .
三、综合题
-
19. 若两个二次函数图象的顶点相同,开口大小相同,但开口方向相反,则称这两个二次函数为“对称二次函数”.(1)、请写出二次函数y=2(x﹣2)2+1的“对称二次函数”;(2)、已知关于x的二次函数y1=x2﹣3x+1和y2=ax2+bx+c,若y1﹣y2与y1互为“对称二次函数”,求函数y2的表达式,并求出当﹣3≤x≤3时,y2的最大值.
四、解答题
-
20.
如图,抛物线y=﹣ x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.

(Ⅰ)求抛物线的解析式及点D的坐标;
(Ⅱ)点F是抛物线上的动点,当∠FBA=∠BDE时,求点F的坐标;
(Ⅲ)若点M是抛物线上的动点,过点M作MN∥x轴与抛物线交于点N,点P在x轴上,点Q在坐标平面内,以线段MN为对角线作正方形MPNQ,请写出点Q的坐标.
21. 湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了 淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养 天的总成本为 万元;放养 天的总成本为 万元(总成本=放养总费用+收购成本).(1)、设每天的放养费用是 万元,收购成本为 万元,求 和 的值;(2)、设这批淡水鱼放养 天后的质量为 ( ),销售单价为 元/ .根据以往经验可知: 与 的函数关系为 ; 与 的函数关系如图所示.
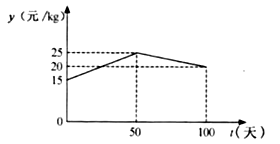
①分别求出当 和 时, 与 的函数关系式;
②设将这批淡水鱼放养 天后一次性出售所得利润为 元,求当 为何值时, 最大?并求出最大值.(利润=销售总额-总成本)
-