人教版数学九年级上册第22章 22.1.1二次函数 同步练习
试卷更新日期:2017-08-24 类型:同步测试
一、单选题
-
1. 某公司今年销售一种产品,一月份获得利润10万元,由于产品畅销,利润逐月增加,一季度共获利36.4万元,已知2月份和3月份利润的月增长率相同.设2,3月份利润的月增长率为x,那么x满足的方程为( )A、10(1+x)2=36.4 B、10+10(1+x)2=36.4 C、10+10(1+x)+10(1+2x)=36.4 D、10+10(1+x)+10(1+x)2=36.42. 为执行“均衡教育”政策,我县2015年投入教育经费2500万元,预计2017年投入3600万元,若每年投入教育经费的年平均增长百分率为x,则下列方程正确的是( )A、2500(1+x)2=3600 B、2500+2500(1+x)+2500(1+x)2=3600 C、2500(1﹣x)2=3600 D、2500(1+x)+2500(1+x)2=36003. 将一块矩形铁皮的四个角各剪去一个边长为1米的正方形后,剩下的部分刚好围成一个容积为15m3的无盖长方体水箱,且此长方体水箱的底面长比宽多2米.求该矩形铁皮的长和宽各是多少米?若设该矩形铁皮的宽是x米,则根据题意可得方程为( )A、(x+2)(x﹣2)×1=15 B、x(x﹣2)×1=15 C、x(x+2)×1=15 D、(x+4)(x﹣2)×1=154. 沅江市近年来大力发展芦笋产业,某芦笋生产企业在两年内的销售额从20万元增加到80万元.设这两年的销售额的年平均增长率为x,根据题意可列方程为( )A、20(1+2x)=80 B、2×20(1+x)=80 C、20(1+x2)=80 D、20(1+x)2=805. 某商品原价800元,连续两次降价a%后售价为578元,下列所列方程正确的是( )A、800(1+a%)2=578 B、800(1﹣a%)2=578 C、800(1﹣2a%)=578 D、800(1﹣a2%)=5786. 心理学家发现:学生对概念的接受能力y与提出概念的时间x(min)之间是二次函数关系,当提出概念13min时,学生对概念的接受力最大,为59.9;当提出概念30min时,学生对概念的接受能力就剩下31,则y与x满足的二次函数关系式为( )A、y=﹣(x﹣13)2+59.9 B、y=﹣0.1x2+2.6x+31 C、y=0.1x2﹣2.6x+76.8 D、y=﹣0.1x2+2.6x+437. 某种品牌运动服经过两次降价,每件零售价由560元降为315元,已知两次降价的百分率相同,求每次降价的百分率.设每次降价的百分率为x,下面所列的方程中正确的是( )A、560(1+x)2=315 B、560(1﹣x)2=315 C、560(1﹣2x)2=315 D、560(1﹣x2)=3158. 两年前生产1吨甲种药品的成本是5000元.随着生产技术的进步,成本逐年下降,第2年的年下降率是第1年的年下降率的2倍,现在生产1吨甲种药品成本是2400元.为求第一年的年下降率,假设第一年的年下降率为x,则可列方程( )A、5000(1﹣x﹣2x)=2400 B、5000(1﹣x)2=2400 C、5000﹣x﹣2x=2400 D、5000(1﹣x)(1﹣2x)=24009. 某种商品的进货检为每件a元,零售价为每件90元,若商品按八五折出售,仍可获利10%,则下列方程正确的是( )A、85%a10%×90 B、90×85%×10%=a C、85%(90﹣a)=10% D、(1+10%)a=90×85%10. 绿苑小区在规划设计时,准备在两幢楼房之间,设置一块面积为900平方米的矩形绿地,并且长比宽多10米.设绿地的宽为x米,根据题意,可列方程为( )A、x(x﹣10)=900 B、x(x+10)=900 C、10(x+10)=900 D、2[x+(x+10)]=900
二、填空题
-
11. 已知二次函数y=ax|a﹣1|+3在对称轴的左侧,y随x的增大而增大,则a= .12. 二次函数y=(m﹣1)x2+x+m2﹣1的图象经过原点,则m的值为 .13. 已知二次函数y=kx2+2x﹣1与x轴有交点,则k的取值范围 .14. 某产品每件成本10元,试销阶段每件产品的销售单价x(元/件)与日销售量y(件)之间的关系如下表.
x(元∕件)
15
18
20
22
…
y(件)
250
220
200
180
…
按照这样的规律可得,日销售利润w(元)与销售单价x(元/件)之间的函数关系式是 .
15. 如图,在Rt△ABC中,∠BAC=90°,AB=AC=2 ,AD为BC边上的高,动点P在AD上,从点A出发,沿A→D方向运动,设AP=x,△ABP的面积为S1 , 矩形PDFE的面积为S2 , y=S1+S2 , 则y与x的关系式是 .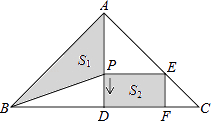
三、解答题
-
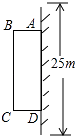
16. 已知函数y=(m﹣2)x +2x﹣1是一个二次函数,求该二次函数的解析式.17. 为了改善小区环境,某小区决定要在一块一边靠墙(墙长25m)的空地上修建一条矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为40m的栅栏围住(如图).若设绿化带BC边长为xm,绿化带的面积为ym2 , 求y与x之间的函数关系式,并写出自变量x的取值范围.
 18. 如图所示,在矩形ABCD中,AB=6厘米,BC=12厘米,点P在线段AB上,P从点A开始沿AB边以1厘米/秒的速度向点B移动.点E为线段BC的中点,点Q从E点开始,沿EC以1厘米/秒的速度向点C移动.如果P、Q同时分别从A、E出发,写出出发时间t与△BPQ的面积S的函数关系式,求出t的取值范围.
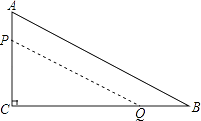
18. 如图所示,在矩形ABCD中,AB=6厘米,BC=12厘米,点P在线段AB上,P从点A开始沿AB边以1厘米/秒的速度向点B移动.点E为线段BC的中点,点Q从E点开始,沿EC以1厘米/秒的速度向点C移动.如果P、Q同时分别从A、E出发,写出出发时间t与△BPQ的面积S的函数关系式,求出t的取值范围.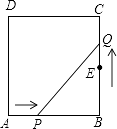 19. 如图,在△ABC中,∠C=90,AC=12cm,BC=24cm,动点P从点A开始沿边AC向点C以2cm/s的速度移动.动点Q从点B开始沿边BC向点C以4cm/s的速度移动,如果P、Q分别从点A、B同时出发,那么△PCQ的面积S随出发时间t如何变化?(写出函数关系式及t的取值范围)
19. 如图,在△ABC中,∠C=90,AC=12cm,BC=24cm,动点P从点A开始沿边AC向点C以2cm/s的速度移动.动点Q从点B开始沿边BC向点C以4cm/s的速度移动,如果P、Q分别从点A、B同时出发,那么△PCQ的面积S随出发时间t如何变化?(写出函数关系式及t的取值范围)