人教版数学九年级上册第21章 21.1一元二次方程同步练习

试卷更新日期：2017-08-24 类型：同步测试

进入出卷网下载

一、单选题

1. 已知x=2是方程x²+bx﹣2=0的一个根，则b的值是（）

A、﹣1 B、1 C、﹣2 D、2

查看试题解析
2. 若x₀是方程ax²+2x+c=0（a≠0）的一个根，设M=1﹣ac，N=（ax₀+1）² ，则M与N的大小关系正确的为（）

A、M＞N B、M=N C、M＜N D、不确定

查看试题解析
3. 已知x=1是方程ax²+bx﹣6=0（a≠0）的一个解，若a≠b，则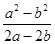的值为（）

A、﹣3 B、3 C、﹣6 D、6

查看试题解析
4. 如果2是方程x²﹣3x+k=0的一个根，则常数k的值为（）

A、1 B、2 C、﹣1 D、﹣2

查看试题解析
5. 三角形的两边a、b的夹角为60°且满足方程x²﹣3 $\sqrt{2}$ x+4=0，则第三边的长是（）

A、 $\sqrt{6}$ B、2 $\sqrt{2}$ C、2 $\sqrt{3}$ D、3 $\sqrt{2}$

查看试题解析
6. 若关于x的一元二次方程（m﹣2）x²﹣2x+1=0有实根，则m的取值范围是（）

A、m＜3 B、m≤3 C、m＜3且m≠2 D、m≤3且m≠2

查看试题解析
7. 若关于y的一元二次方程ky²﹣4y﹣3=3y+4有实根，则k的取值范围是（）

A、k＞﹣ $\frac{7}{4}$ B、k≥﹣ $\frac{7}{4}$ 且k≠0 C、k≥﹣ $\frac{7}{4}$ D、k＞ $\frac{7}{4}$ 且k≠0

查看试题解析
8. 已知关于x的一元二次方程mx²+3x﹣4=3x²有两个不相等的实数根，则m的值可以是（）

A、4 B、3 C、2 D、0

查看试题解析
9. 已知关于x的方程（k﹣1）x²﹣2x+1=0有实数根，则k的取值范围是（）

A、k≤﹣2 B、k≤2 C、k≥2 D、k≤2且k≠1

查看试题解析
10. 若关于x的一元二次方程mx²﹣2x+1=0有实数根，则实数m的取值范围是（）

A、m≥1 B、m≤1 C、m≥1且m≠0 D、m≤1且m≠0

查看试题解析
11. 已知关于x的一元二次方程：（a﹣1）x²﹣ax+1=0有两个相等的实数根，则a的值应为下列哪个值（）

A、2 B、1 C、2或1 D、无法确定

查看试题解析
12. 我们知道方程x²+2x﹣3=0的解是x₁=1，x₂=﹣3，现给出另一个方程（2x+3）²+2（2x+3）﹣3=0，它的解是（）

A、x₁=1，x₂=3 B、x₁=1，x₂=﹣3 C、x₁=﹣1，x₂=3 D、x₁=﹣1，x₂=﹣3

查看试题解析

二、填空题

13. 方程x= $\sqrt{4 - 3 x}$ 的根是．

查看试题解析
14. 方程 $\sqrt{x - 1}$ =1的解为．

查看试题解析
15. 定义新运算：a*b=a（b﹣1），若a、b是关于一元二次方程x²﹣x+ $\frac{1}{4}$ m=0的两实数根，则b*b﹣a*a的值为．

查看试题解析
16. 如果t是方程x²﹣2x﹣1=0的根，那么代数式2t²﹣4t的值是．

查看试题解析
17. 若关于x的方程（a+3）x^|^a^|^﹣¹﹣3x+2=0是一元二次方程，则a的值为．

查看试题解析

三、计算题

18. 若（m+1）x^|^m^|+¹+6x﹣2=0是关于x的一元二次方程，求m的值．

查看试题解析
19. 方程 $(m - 2) x^{m^{2} - 2} + (3 - m) x - 2 = 0$ 是一元二次方程，试求代数式m²+2m﹣4的值．

查看试题解析

四、解答题

20. 先化简，再求值： $(x + 1 - \frac{3}{x - 1}) \div \frac{x^{2} - 4 x + 4}{x - 1}$ ，其中x满足方程：x²+x﹣6=0．

查看试题解析
21. 一元二次方程x²﹣2x﹣ $\frac{5}{4}$ =0的某个根，也是一元二次方程x²﹣（k+2）x+ $\frac{9}{4}$ =0的根，求k的值．

查看试题解析
22. 已知关于x的方程（k﹣1）x²﹣（k﹣1）x+ $\frac{1}{4}$ =0有两个相等的实数根，求k的值．

查看试题解析

人教版数学九年级上册第21章 21.1一元二次方程 同步练习

一、单选题

二、填空题

三、计算题

四、解答题

人教版数学九年级上册第21章 21.1一元二次方程同步练习