河北省遵化市2020年中考数学一模考试试卷

试卷更新日期：2020-03-17 类型：中考模拟

进入出卷网下载

一、选择题

1. 如图，数轴上有三个点A、B、C，若点A、B表示的数互为相反数，则图中点C对应的数是（）

A、﹣2 B、0 C、1 D、4

查看试题解析
2. 肥皂泡的泡壁厚度大约是0.0007mm，0.0007用科学记数法表示为（　　）

A、0.7×10^﹣³ B、7×10^﹣³ C、7×10^﹣⁴ D、7×10^﹣⁵

查看试题解析
3. 如图将一块三角尺的直角顶点放在直尺的一边上，当∠1＝35°时，∠2的度数为（）

A、35° B、45° C、55° D、65°

查看试题解析
4. 下列计算中，不正确的是（）

A、 $a^{2} \cdot a^{5} = a^{10}$ B、 $a^{2} - 2 a b + b^{2} = {(a - b)}^{2}$ C、 $- (a - b) = b - a$ D、 $3 a^{3} b^{2} \div a^{2} b^{2} = 3 a$

查看试题解析
5. 如图所示，用量角器度量∠AOB，可以读出∠AOB的度数为（）

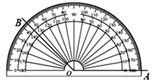A、145° B、135° C、55° D、45°

查看试题解析
6. 计算 $\frac{{(x + y)}^{2} - {(x - y)}^{2}}{4 x y}$ 的结果为（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、1 D、0

查看试题解析
7. 边长为5的菱形ABCD按如图所示放置在数轴上，其中A点表示数﹣2，C点表示数6，则BD=（）

A、4 B、6 C、8 D、10

查看试题解析
8. 下列说法正确的是（）

A、“367人中有2人同月同日生”为必然事件 B、检测某批次灯泡的使用寿命，适宜用全面调查 C、可能性是1%的事件在一次试验中一定不会发生 D、数据3，5，4，1，-2的中位数是4

查看试题解析
9. 如图，在△ABC与△ADE中，∠BAC＝∠D，要使△ABC与△ADE相似，还需满足下列条件中的（）

A、 $\frac{A C}{A D}$ ＝ $\frac{A B}{A E}$ B、 $\frac{A C}{A D}$ ＝ $\frac{B C}{D E}$ C、 $\frac{A C}{A D}$ ＝ $\frac{A B}{D E}$ D、 $\frac{A C}{A D}$ ＝ $\frac{B C}{A E}$

查看试题解析
10. 一次函数y=kx﹣1的图像经过点P，且y的值随x值的增大而增大，则点P的坐标可以为（）

A、（﹣5，3） B、（1，﹣3） C、（2，2） D、（5，﹣1）

查看试题解析
11. A.B两地相距180km，新修的高速公路开通后，在A，B两地间行驶的长途客车平均车速提高了50%，而从A地到B地的时间缩短了1h.若设原来的平均车速为xkm/h，则根据题意可列方程为（）

A、 $\frac{180}{x} - \frac{180}{(1 + 50 %) x} = 1$ B、 $\frac{180}{(1 + 50 %) x} - \frac{180}{x} = 1$ C、 $\frac{180}{x} - \frac{180}{(1 - 50 %) x} = 1$ D、 $\frac{180}{(1 - 50 %) x} - \frac{180}{x} = 1$

查看试题解析
12. 如图，在△ABC中，AB=AC，AD是高，AM是△ABC外角∠CAE的平分线.以点D为圆心，适当长为半径画弧，交DA于点G，交DC于点H.再分别以点G、H为圆心，大于 $\frac{1}{2}$ GH的长为半径画弧，两弧在∠ADC内部交于点Q，连接DQ并延长与AM交于点F，则△ADF的形状是（）

A、等腰三角形 B、等边三角形 C、直角三角形 D、等腰直角三角形

查看试题解析
13. 如图，二次函数y＝ax²＋bx＋c（a≠0）的图像的顶点在第一象限，且过点（0，1）和（－1，0），下列结论：
①ab＜0，②b²-4ac＞0， ③a-b+c＜0， ④c=1， ⑤当x＞－1时，y＞0.
其中正确结论的个数是（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
14. 如图，一个边长为4cm的等边三角形ABC的高与⊙O的直径相等．⊙O与BC相切于点C ，与AC相交于点E ，则CE的长为（　　）

A、4cm B、3cm C、2cm D、1.5cm

查看试题解析
15. 某工厂加工一批零件，为了提高工人工作的积极性，工厂规定每名工人每次获得的薪金如下：生产的零件不超过a件，则每件3元，超过a件，超过部分每件b元，如图是一名工人一天获得薪金y（元）与其生产的件数x（件）之间的函数关系式，则下列结论错误的是（）

A、a=20 B、b=4 C、若工人甲一天获得薪金180元，则他共生产50件 D、若工人乙一天生产m件，则他获得薪金4m元

查看试题解析
16. 如图，一次函数与x轴，y轴的交点分别是A（－4，0），B（0，2）.与反比例函数的图象交于点Q，反比例函数图象上有一点P满足：① PA⊥x轴；②PO＝ $\sqrt{17}$ （O为坐标原点），则四边形PAQO的面积为（）

A、7 B、10 C、4+2 $\sqrt{3}$ D、4-2 $\sqrt{3}$

查看试题解析

二、填空题

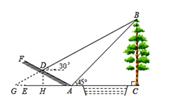
17. 已知 $a$ 、 $b$ 满足 $| a - \frac{1}{2} | + \sqrt{b - 2} = 0$ ，则 $a^{2} b =$ .

查看试题解析
18. 如图，小明为了测量小河对岸大树BC的高度，他在点A测得大树顶端B的仰角是 $45 °$ ，沿斜坡走 $2 \sqrt{5}$ 米到达斜坡上点D ，在此处测得树顶端点B的仰角为 $30 °$ ，且斜坡AF的坡比为1：2.则小明从点A走到点D的过程中，他上升的高度为米；大树BC的高度为米（结果保留根号）.

查看试题解析
19. 将一列有理数－1，2，－3，4，－5，6，……，按如图所示有序排列，

根据图中的排列规律可知，“峰1”中峰顶的位置（C的位置）是有理数4，那么，

(1)、“峰6”中D的位置是有理数；

(2)、2018应排在A，B，C，D，E中的位置.

查看试题解析

三、解答题：（本大题共7个小题；共67分；解答时应写出文字说明、证明过程或演算步骤.）

20. 定义新运算：对于任意实数m、n都有m☆n=m²n+n，等式右边是常用的加法、减法、乘法及乘方运算.
例如：﹣3☆2=（﹣3）²×2+2=20.

根据以上知识解决问题：

(1)、x☆4=20，求x；

(2)、若2☆a的值小于0，请判断方程：2x²﹣bx+a=0的根的情况.

查看试题解析
21. 如图，已知△ABC，直线PQ垂直平分AC，与边AB交于E，连接CE，过点C作CF平行于BA交PQ于点F，连接AF.

(1)、求证：△AED≌△CFD；

(2)、求证：四边形AECF是菱形；

查看试题解析
22. 如图，一次函数y＝kx＋b与反比例函数y＝ $\frac{m}{x}$ .（其中mk≠0）图像交于A（－4，2），B（2，n）两点.

(1)、求一次函数和反比例函数的表达式；

(2)、求△ABO的面积；

(3)、请写出当一次函数值大于反比例函数值时x的取值范围.

查看试题解析
23. 现有甲、乙、丙等多家食品公司在某市开设蛋糕店，该市蛋糕店数量的扇形统计图如图所示，其中统计图中没有标注相应公司数量的百分比．已知乙公司经营150家蛋糕店，请根据该统计图回答下列问题：

(1)、求甲公司经营的蛋糕店数量和该市蛋糕店的总数．

(2)、甲公司为了扩大市场占有率，决定在该市增设蛋糕店，在其余蛋糕店数量不变的情况下，若要使甲公司经营的蛋糕店数量达到全市的20%，求甲公司需要增设的蛋糕店数量．

查看试题解析
24. 如图，在△ABC中，AB＝AC，O是边AC上的点，以OC为半径的圆分别交边BC、AC于点D、E，过点D作DF⊥AB于点F.

(1)、求证：直线DF是⊙O的切线；

(2)、若OC＝1，∠A＝45°，求劣弧DE的长.

查看试题解析
25. 图1是某浴室花洒实景图，图2是该花洒的侧面示意图.已知活动调节点B可以上下调整高度，离地面CD的距离BC＝160cm.设花洒臂与墙面的夹角为α，可以扭动花洒臂调整角度，且花洒臂长AB＝30cm.假设水柱AE垂直AB直线喷射，小华在离墙面距离CD＝120cm处淋浴.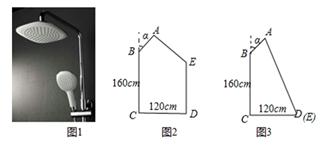

(1)、当α＝30°时，水柱正好落在小华的头顶上，求小华的身高DE.

(2)、如果小华要洗脚，需要调整水柱AE，使点E与点D重合，调整的方式有两种：
①其他条件不变，只要把活动调节点B向下移动即可，移动的距离BF与小华的身高DE有什么数量关系？直接写出你的结论；

②活动调节点B不动，只要调整α的大小，在图3中，试求α的度数.

（参考数据： $\sqrt{3}$ ≈1.73，sin8.6°≈0.15，sin36.9°≈0.60，tan36.9°≈0.75）

查看试题解析
26. 如图，直线OA与反比例函数的图象交于点A（3，3），向下平移直线OA，与反比例函数的图象交于点B（6，m）与y轴交于点C，

(1)、求直线BC的解析式；

(2)、求经过A、B、C三点的二次函数的解析式；

(3)、设经过A、B、C三点的二次函数图象的顶点为D，对称轴与x轴的交点为E.
问：在二次函数的对称轴上是否存在一点P，使以O、E、P为顶点的三角形与△BCD相似？若存在，请求出点P的坐标；若不存在，请说明理由.

查看试题解析