福建省宁德市2016-2017学年中考数学模拟考试试卷

试卷更新日期：2017-08-23 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣3的绝对值是（）

A、3 B、 $\frac{1}{3}$ C、 $- \frac{1}{3}$ D、﹣3

查看试题解析
2. 已知一个几何体的三种视图如图所示，则该几何体是（）

A、三棱柱 B、三棱锥 C、圆锥 D、圆柱

查看试题解析
3.
如图，点M在线段AB上，则下列条件不能确定M是AB中点的是（）

A、BM= $\frac{1}{2}$ AB B、AM+BM=AB C、AM=BM D、AB=2AM

查看试题解析
4. 在△ABC中，AB=5，AC=8，则BC长不可能是（）

A、4 B、8 C、10 D、13

查看试题解析
5. 下列计算正确的是（）

A、﹣5+2=﹣7 B、6÷（﹣2）=﹣3 C、（﹣1）²⁰¹⁷=1 D、﹣2⁰=1

查看试题解析
6.
如图所示的分式化简，对于所列的每一步运算，依据错误的是（）

A、①：同分母分式的加减法法则 B、②：合并同类项法则 C、③：提公因式法 D、④：等式的基本性质

查看试题解析
7.
某创意工作室6位员工的月工资如图所示，因业务需要，现决定招聘一名新员工，若新员工的工资为4500元，则下列关于现在7位员工工资的平均数和方差的说法正确的是（）

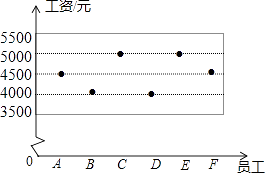A、平均数不变，方差变大 B、平均数不变，方差变小 C、平均数不变，方差不变 D、平均数变小，方差不变

查看试题解析
8.
如图，直线ι是一次函数y=kx+b的图象，若点A（3，m）在直线ι上，则m的值是（）

A、﹣5 B、 $\frac{3}{2}$ C、 $\frac{5}{2}$ D、7

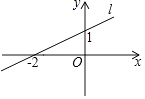查看试题解析
9. 函数y=x³﹣3x的图象如图所示，则以下关于该函数图象及其性质的描述正确的是（）

A、函数最大值为2 B、函数图象最低点为（1，﹣2） C、函数图象关于原点对称 D、函数图象关于y轴对称

查看试题解析
10. 如图，在△ABC中，AB=AC，点D，E分别在边BC 和AC上，若AD=AE，则下列结论错误的是（）

A、∠ADB=∠ACB+∠CAD B、∠ADE=∠AED C、∠CDE= $\frac{1}{2}$ ∠BAD D、∠AED=2∠ECD

查看试题解析

二、填空题

11. 2016年9月26日，我国自主设计建造的世界最大球面射电望远镜落成启用．该望远镜理论上能接收到13 700 000 000光年以外的电磁信号．数据13 700 000 000光年用科学记数法表示为光年．

查看试题解析
12. 一元二次方程x（x+3）=0的根是．

查看试题解析
13. 若矩形的面积为a²+ab，长为a+b，则宽为．

查看试题解析
14. 甲、乙两位同学参加物理实验考试，若每人只能从A、B、C、D四个实验中随机抽取一个，则甲、乙两位同学抽到同一实验的概率为．

查看试题解析
15.
将边长为2的正六边形ABCDEF绕中心O顺时针旋转α度与原图形重合，当α最小时，点A运动的路径长为．

查看试题解析
16.
如图，在平面直角坐标系中，菱形OABC的边OA在x轴上，AC与OB交于点D （8，4），反比例函数y= $\frac{k}{x}$ 的图象经过点D．若将菱形OABC向左平移n个单位，使点C落在该反比例函数图象上，则n的值为．

查看试题解析

三、解答题

17. 化简并求值：x（x﹣2）+（x+1）² ，其中x=﹣2．

查看试题解析
18. 已知：不等式 $\frac{2 - x}{3}$ ≤2+x

(1)、解该不等式，并把它的解集表示在数轴上；

(2)、若实数a满足a＞2，说明a是否是该不等式的解．

查看试题解析
19. 如图，E，F为平行四边形ABCD的对角线BD上的两点，AE⊥BD于点E，CF⊥BD于点F．
求证：AE=CF．

查看试题解析
20. 小明作业本中有一页被墨水污染了，已知他所列的方程组是正确的．写出题中被墨水污染的条件，并求解这道应用题．

查看试题解析
21. 某初中学校组织200位同学参加义务植树活动，每人植树的棵数在5至10之间．甲、乙两位同学分别调查了30位同学的植树情况，并将收集的数据进行了整理，绘制成统计表分别为表1和表2：
表1：甲调查九年级30位同学植树情况统计表（单位：棵）
每人植树情况
7
8
9
10
人数
3
6
15
6
频率
0.1
0.2
0.5
0.2
表2：乙调查三个年级各10位同学植树情况统计表（单位：棵）
每人植树情况
6
7
8
9
10
人数
3
6
3
11
6
频率
0.1
0.2
0.1
0.4
0.2
根据以上材料回答下列问题：

(1)、表1中30位同学植树情况的中位数是棵；

(2)、已知表2的最后两列中有一个错误的数据，这个错误的数据是，正确的数据应该是

(3)、指出哪位同学所抽取的样本能更好反映此次植树活动情况，并用该样本估计本次活动200位同学一共植树多少棵？

查看试题解析
22.
如图，在边长为1的正方形组成的5×8方格中，△ABC的顶点都在格点上．

(1)、在给定的方格中，以直线AB为对称轴，画出△ABC的轴对称图形△ABD．

(2)、求sin∠ABD的值．

查看试题解析
23.
如图，BF为⊙O的直径，直线AC交⊙O于A，B两点，点D在⊙O上，BD平分∠OBC，DE⊥AC于点E．

(1)、求证：直线DE是⊙O的切线；

(2)、若 BF=10，sin∠BDE= $\frac{\sqrt{5}}{5}$ ，求DE的长．

查看试题解析
24. 在平面直角坐标系中，点A的坐标为（0，3），点B和点D的坐标分别为（m，0），（n，4），且m＞0，四边形ABCD是矩形．

(1)、
如图1，当四边形ABCD为正方形时，求m，n的值；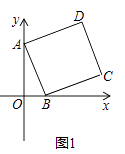

(2)、
在图2中，画出矩形ABCD，简要说明点C，D的位置是如何确定的，并直接用含m的代数式表示点C的坐标；

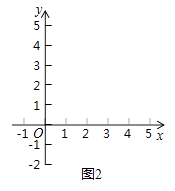(3)、探究：当m为何值时，矩形ABCD的对角线AC的长度最短．

查看试题解析
25.
如图，抛物线l：y= $\frac{1}{2}$ （x﹣h）²﹣2与x轴交于A，B两点（点A在点B的左侧），将抛物线ι在x轴下方部分沿轴翻折，x轴上方的图象保持不变，就组成了函数ƒ的图象．

(1)、若点A的坐标为（1，0）．
①求抛物线l的表达式，并直接写出当x为何值时，函数ƒ的值y随x的增大而增大；
②如图2，若过A点的直线交函数ƒ的图象于另外两点P，Q，且S_△ABQ=2S_△ABP ，求点P的坐标；

(2)、当2＜x＜3时，若函数f的值随x的增大而增大，直接写出h的取值范围．

查看试题解析

每人植树情况	7	8	9	10
人数	3	6	15	6
频率	0.1	0.2	0.5	0.2

每人植树情况	6	7	8	9	10
人数	3	6	3	11	6
频率	0.1	0.2	0.1	0.4	0.2