北京市东城区2016-2017学年中考数学二模考试试卷

试卷更新日期：2017-08-23 类型：中考模拟

进入出卷网下载

一、选择题

1. 中国倡导的“一带一路”建设将促进我国与世界各国的互利合作，根据规划，“一带一路”地区覆盖总人口约为440000万人，将440000用科学记数法表示为（）

A、4.4×10⁶ B、4.4×10⁵ C、44×10⁴ D、0.44×10⁵

查看试题解析
2. 下列运算正确的是（）

A、2a+3b=5ab B、a¹•a⁴=a⁶ C、（a²b）³=a⁶b³ D、（a+2）²=a²+4

查看试题解析
3. 有5张看上去无差别的卡片，上面分别写着0，π， $\sqrt{2}$ ， $\frac{1}{8}$ ，1.333，背面朝上放在不透明的桌子上，若随机抽取1张，则取出的卡片上的数是无理数的概率是（）

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
4. 下列关于二次函数y=x²+2x+3的最小值的描述正确的是（）

A、有最小值是2 B、有最小值是3 C、有最大值是2 D、有最大值是3

查看试题解析
5. 学校准备从甲、乙、丙、丁四个科创小组中选出一组代表学校参加青少年科技创新大赛，各组的平时成绩的平均数 $\bar{x}$ （单位：分）及方差s²如表所示：
甲
乙
丙
丁
$\bar{x}$
7
8
8
7
s²
1
1.2
1
1.8
如果要选出一个成绩较好且状态稳定的组去参赛，那么应选的组是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
6. 如图，正五边形ABCDE放入某平面直角坐标系后，若顶点A、B、C、D、E的坐标分别是（0，a）、（﹣3，2）、（b，m）、（﹣b，m），则点E的坐标是（）

A、（2，﹣3） B、（2，3） C、（3，2） D、（3，﹣2）

查看试题解析
7. 将一副直角三角板如图放置，使含30°角的三角板的直角边和含45°角的三角板的一条直角边在同一条直线上，则∠1的度数为（）

A、75° B、65° C、45° D、30°

查看试题解析
8. 关于x的一元二次方程x²+ax﹣1=0的根的情况是（）

A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根

查看试题解析
9.
图1和图2中所有的正方形都全等，将图1的正方形放在图2中的①②③④某一位置，所组成的图形不能围成正方体的位置是（）

A、① B、② C、③ D、④

查看试题解析
10.
如图，点E为菱形ABCD的BC边的中点，动点F在对角线AC上运动，连接BF、EF，设AF=x，△BEF的周长为y，那么能表示y与x的函数关系的大致图象是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 代数式 $\frac{1}{x - 3}$ 在实数范围内有意义，则x的取值范围是

查看试题解析
12. 请写出一个多项式，含有字母a，并能够在有理数范围内用平方差公式进行因式分解，此多项式可以是．

查看试题解析
13. 已知一次函数y₁=k₁x+5和y₂=k₂x+7，若k₁＞0，且k₂＜0，则这两个一次函数的图象的交点在第象限．

查看试题解析
14. 如图，⊙O的半径为4，△ABC是⊙O的内接三角形，连接OB、OC，若∠BAC和∠BOC互补，则弦BC的长度为．

查看试题解析
15. 如图，一扇形纸扇完全打开后，外侧两竹条AB和AC的夹角为120°，竹条AB的长为25cm，贴纸部分的宽BD为15cm，若纸扇两面贴纸，则一面贴纸的面积为cm²（结果保留π）．

查看试题解析
16.
小明在他家里的时钟上安装了一个电脑软件，他设定当钟声在n点钟响起后，下一次则在（3n﹣1）小时后响起，例如钟声第一次在3点钟响起，那么第2次在（3×3﹣1=8）小时后，也就是11点响起，第3次在（3×11﹣1=32）小时后，即7点响起，以此类推…；现在第1次钟声响起时为2点钟，那么第3次响起时为点，第2017次响起时为点（如图钟表，时间为12小时制）．

查看试题解析

三、解答题

17. 计算：|﹣2|+（π﹣2017）⁰﹣4cos60°+ $\sqrt{27}$ ．

查看试题解析
18. 解不等式组 ${\begin{matrix} 3 x - 2 \leq x \\ \frac{2 x + 1}{5} < \frac{x + 1}{2} \end{matrix}$ ，并把解集在数轴上表示出来．

查看试题解析
19. 小明化简（2x+1）（2x﹣1）﹣x（x+5）的过程如图，请指出他化简过程中的错误，写出对应的序号，并写出正确的化简过程．
解：原式=2x²﹣1﹣x（x+5）…①
=2x²﹣1﹣x²+5x…②
=x²+5x﹣1 …③

查看试题解析
20. 如图，在Rt△ABC中，∠C=90°，以顶点A为圆心，适当长为半径画弧，分别交AC、AB于点M、N，再分别以点M、N为圆心，大于 $\frac{1}{2}$ MN的长为半径画弧，两弧交于点P，作射线AP交变BC于点D，若CD=4，AB=15，求△ABD的面积．

查看试题解析
21.
如图，在平面直角坐标系中，OA⊥OB，AB⊥x轴于点C，点A（ $\sqrt{3}$ ，1）在反比例函数y= $\frac{k}{x}$ （x≠0）的图象上．

(1)、求反比例函数y= $\frac{k}{x}$ （x≠0）的解析式和点B的坐标；

(2)、若将△BOA绕点B按逆时针方向旋转60°得到△BDE（点O与点D是对应点），补全图形，直接写出点E的坐标，并判断点E是否在该反比例函数的图象上，说明理由．

查看试题解析
22. 列方程或方程组解应用题：
某校为美化校园，计划对一些区域进行绿化，安排了甲、乙两个工程队完成，已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍，并且两队在独立完成面积为400m²区域的绿化时，甲队比乙队少用4天，求甲、乙两工程队每天能完成绿化的面积分别是多少m²？

查看试题解析
23. 如图，BD是△ABC的角平分线，它的垂直平分线分别交AB、BC于点E、F、G，连接ED、DG．

(1)、请判断四边形EBGD的形状，并说明理由；

(2)、若∠ABC=30°，∠C=45°，ED=2，求GC的长．

查看试题解析
24.
某市为提倡节约用水，准备实行自来水“阶梯计费”方式，用户用水不超出基本用水量的部分享受基本价格，超出基本用水量的部分实行加价收费，为更好地做决策，自来水公司随机抽取部分用户的用水量数据，并绘制了如图不完整的统计图（每组数据包括右端点但不包括左端点），请你根据统计图解决下列问题：

(1)、此次抽样调查的样本容量是．

(2)、补全频数分布直方图．

(3)、如果自来水公司将基本用水量定为每户25吨，那么该地区6万用户中约有多少用户的用水全部享受基本价格？

查看试题解析
25. 如图，AB是⊙O的直径，点C在AB的延长线上，CD与⊙O相切于点D，CE⊥AD，交AD的延长线于点E．

(1)、求证：∠BDC=∠A；

(2)、若CE=4，DE=2，求AD的长．

查看试题解析
26. 佳佳向探究一元三次方程x³+2x²﹣x﹣2=0的解的情况，根据以往的学习经验，他想到了方程与函数的关系，一次函数y=kx+b（k≠0）的图象与x轴交点的横坐标即为一元一次方程kx+b（k≠0）的解，二次函数y=ax²+bx+c（a≠0）的图象与x轴交点的横坐标即为一元二次方程ax²+bx+c=0（a≠0）的解，如：二次函数y=x²﹣2x﹣3的图象与x轴的交点为（﹣1，0）和（3，0），交点的横坐标﹣1和3即为x²﹣2x﹣3=0的解．
根据以上方程与函数的关系，如果我们直到函数y=x³+2x²﹣x﹣2的图象与x轴交点的横坐标，即可知方程x³+2x²﹣x﹣2=0的解．
佳佳为了解函数y=x³+2x²﹣x﹣2的图象，通过描点法画出函数的图象．
x
…
﹣3
﹣ $\frac{5}{2}$
﹣2
﹣ $\frac{3}{2}$
﹣1
﹣ $\frac{1}{2}$
0
$\frac{1}{2}$
1
$\frac{3}{2}$
2
…
y
…
﹣8
﹣ $\frac{21}{8}$
0
$\frac{5}{8}$
m
﹣ $\frac{9}{8}$
﹣2
﹣ $\frac{15}{8}$
0
$\frac{35}{8}$
12
…

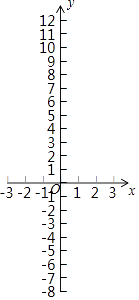(1)、直接写出m的值，并画出函数图象；

(2)、根据表格和图象可知，方程的解有个，分别为；

(3)、借助函数的图象，直接写出不等式x³+2x²＞x+2的解集．

查看试题解析
27. 在平面直角坐标系xOy中，抛物线y=﹣x²+2mx﹣m²﹣m+1

(1)、当抛物线的顶点在x轴上时，求该抛物线的解析式；

(2)、不论m取何值时，抛物线的顶点始终在一条直线上，求该直线的解析式；

(3)、若有两点A（﹣1，0），B（1，0），且该抛物线与线段AB始终有交点，请直接写出m的取值范围．

查看试题解析
28.
取一张正方形的纸片进行折叠，具体操作过程如下：
第一步：如图1，先把正方形ABCD对折，折痕为MN．
第二步：点G在线段 MD上，将△GCD沿GC翻折，点D恰好落在MN上，记为点P，连接BP．

(1)、判断△PBC的形状，并说明理由；

(2)、
作点C关于直线AP的对称点C′，连接PC′、DC′．
①在图2中补全图形，并求出∠APC′的度数；
②猜想∠PC′D的度数，并加以证明；（温馨提示：当你遇到困难时，不妨连接AC′、CC′，研究图形中特殊的三角形）

查看试题解析
29. 在平面直角坐标系xOy中，点P与点Q不重合，以点P为圆心作经过Q的圆，则称该圆为点P、Q的“相关圆”

(1)、已知点P的坐标为（2，0）
①若点Q的坐标为（0，1），求点P、Q的“相关圆”的面积；
②若点Q的坐标为（3，n），且点P、Q的“相关圆”的半径为 $\sqrt{5}$ ，求n的值；

(2)、已知△ABC为等边三角形，点A和点B的坐标分别为（﹣ $\sqrt{3}$ ，0）、（ $\sqrt{3}$ ，0），点C在y轴正半轴上，若点P、Q的“相关圆”恰好是△ABC的内切圆且点Q在直线y=2x上，求点Q的坐标．

(3)、已知△ABC三个顶点的坐标为：A（﹣3，0）、B（ $\frac{9}{2}$ ，0），C（0，4），点P的坐标为（0， $\frac{3}{2}$ ），点Q的坐标为（m， $\frac{3}{2}$ ），若点P、Q的“相关圆”与△ABC的三边中至少一边存在公共点，直接写出m的取值范围．

查看试题解析

	甲	乙	丙	丁
$\bar{x}$	7	8	8	7
s²	1	1.2	1	1.8