浙江省台州市玉环县2016-2017学年中考模拟数学考试试卷
试卷更新日期:2017-08-23 类型:中考模拟
一、选择题
-
1. 3的绝对值是( )A、3 B、﹣3 C、±3 D、2. 在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下面四个几何体中,左视图是四边形的几何体共有( )
3. 下面四个几何体中,左视图是四边形的几何体共有( ) A、1个 B、2个 C、3个 D、4个4. 某商场试销一种新款衬衫,一周内销售情况如下表所示:商场经理要了解哪种型号最畅销,则上述数据的统计量中,对商场经理来说最有意义的是( )
A、1个 B、2个 C、3个 D、4个4. 某商场试销一种新款衬衫,一周内销售情况如下表所示:商场经理要了解哪种型号最畅销,则上述数据的统计量中,对商场经理来说最有意义的是( )型号(厘米)
38
39
40
41
42
43
数量(件)
25
30
36
50
28
8
A、平均数 B、众数 C、中位数 D、方差5. 如图,给出下列四个条件,AB=DE,BC=EF,∠B=∠E,∠C=∠F,从中任选三个条件能使△ABC≌△DEF的共有( ) A、1组 B、2组 C、3组 D、4组6. 关于x的一元二次方程mx2+2x+1=0有两个不相等的实数根,则m的取值范围是( )A、m<1 B、m≤1 C、m<1且m≠0 D、m≤1且m≠07. 数轴上A点读数为﹣1,B点读为3,点C在数轴上,且AC+BC=6,则C点的读数为( )A、﹣2 B、4 C、﹣2或4 D、﹣3或58. 如图,O是坐标原点,菱形OABC的顶点A的坐标为(﹣3,4),顶点C在x轴的负半轴上,函数y= (x<0)的图象经过顶点B,则k的值为( )
A、1组 B、2组 C、3组 D、4组6. 关于x的一元二次方程mx2+2x+1=0有两个不相等的实数根,则m的取值范围是( )A、m<1 B、m≤1 C、m<1且m≠0 D、m≤1且m≠07. 数轴上A点读数为﹣1,B点读为3,点C在数轴上,且AC+BC=6,则C点的读数为( )A、﹣2 B、4 C、﹣2或4 D、﹣3或58. 如图,O是坐标原点,菱形OABC的顶点A的坐标为(﹣3,4),顶点C在x轴的负半轴上,函数y= (x<0)的图象经过顶点B,则k的值为( ) A、﹣12 B、﹣27 C、﹣32 D、﹣369. 如图,在正方形ABCD中,AD=5,点E、F是正方形ABCD内的两点,且AE=FC=3,BE=DF=4,则EF的长为( )
A、﹣12 B、﹣27 C、﹣32 D、﹣369. 如图,在正方形ABCD中,AD=5,点E、F是正方形ABCD内的两点,且AE=FC=3,BE=DF=4,则EF的长为( )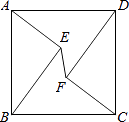 A、 B、 C、 D、10.
A、 B、 C、 D、10.农夫将苹果树种在正方形的果园内.为了保护苹果树不怕风吹,他在苹果树的周围种针叶树.在下图里,你可以看到农夫所种植苹果树的列数(n)和苹果树数量及针叶树数量的规律:当n为某一个数值时,苹果树数量会等于针叶树数量,则n为( )
 A、6 B、8 C、12 D、16
A、6 B、8 C、12 D、16二、填空题
-
11. 分解因式:3a2﹣12= .12. 不等式组 的解集为 .13. 设a<b<0,a2+b2=4ab,则 的值为 .14. 如图,△ABC的各个顶点都在正方形的格点上,则sinA的值为
 15. 以A为圆心,半径为9的四分之一圆,与以C为圆心,半径为4的四分之一圆如图所示放置,且∠ABC=90°,则图中阴影部分的面积为 .
15. 以A为圆心,半径为9的四分之一圆,与以C为圆心,半径为4的四分之一圆如图所示放置,且∠ABC=90°,则图中阴影部分的面积为 .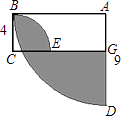 16. 如图,点E,F分别是矩形ABCD的边BC和CD上的点,其中AB=3 ,BC=3 ,把△ABE沿AE进行折叠,使点B落在对角线AC上,在把△ADF沿AF折叠,使点D落在对角线AC上,点P为直线AF上任意一点,则PE的最小值为 .
16. 如图,点E,F分别是矩形ABCD的边BC和CD上的点,其中AB=3 ,BC=3 ,把△ABE沿AE进行折叠,使点B落在对角线AC上,在把△ADF沿AF折叠,使点D落在对角线AC上,点P为直线AF上任意一点,则PE的最小值为 .
三、解答题
-
17. 根据问题填空:(1)、计算:|﹣3|+tan60°+ ;(2)、化简:(x﹣1)2+x(x+1).18. 先化简再求值:(x﹣1)2﹣x(x+2)﹣ ,其中x= .19. 如图,在▱ABCD中,BD是对角线,且DB⊥BC,E、F分别为边AB、CD的中点.求证:四边形DEBF是菱形.
 20. 如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4米.
20. 如图是某货站传送货物的平面示意图.为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°.已知原传送带AB长为4米.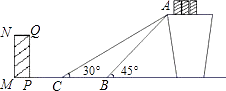 (1)、求新传送带AC的长度;(2)、如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物MNQP是否需要挪走,并说明理由.(说明:(1)(2)的计算结果精确到0.1米,参考数据: ≈1.41, ≈1.73, ≈2.24, ≈2.45)21. “端午节”所示我国的传统佳节,民间历来有吃“粽子”的习俗,我市某食品厂为了解市民对去年销售较好的肉馅棕、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不用口味粽子的喜爱情况,在节前对某居民区进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).
(1)、求新传送带AC的长度;(2)、如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物MNQP是否需要挪走,并说明理由.(说明:(1)(2)的计算结果精确到0.1米,参考数据: ≈1.41, ≈1.73, ≈2.24, ≈2.45)21. “端午节”所示我国的传统佳节,民间历来有吃“粽子”的习俗,我市某食品厂为了解市民对去年销售较好的肉馅棕、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不用口味粽子的喜爱情况,在节前对某居民区进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).
请根据以上信息回答:
(1)、本次参加抽样调查的居民有多少人?(2)、将两幅不完整的图补充完整;(3)、若居民区有8000人,请估计爱吃D粽的人数;(4)、若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个,用列表或画树状图的方法,求他第二个恰好吃到的是C粽的概率.22. 已知△ABE中,∠BAE=90°,以AB为直径作⊙O,与BE边相交于点C,过点C作⊙O的切线CD,交AE于点D.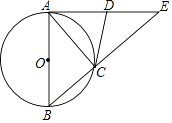 (1)、求证:D是AE的中点;(2)、求证:AE2=EC•EB.23.
(1)、求证:D是AE的中点;(2)、求证:AE2=EC•EB.23.如图①,OP为一墙面,它与地面OQ垂直,有一根木棒AB如图放置,点C是它的中点,现在将木棒的A点在OP上由A点向下滑动,点B由O点向OQ方向滑动,直到AB横放在地面为止.
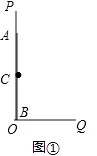 (1)、
(1)、在AB滑动过程中,点C经过的路径可以用下列哪个图象来描述( )
 (2)、
(2)、若木棒长度为2m,如图②射线OM与地面夹角∠MOQ=60°,当AB滑动过程中,与OM并于点D,分别求出当AD= 、AD=1、AD= 时,OD的值.
 (3)、
(3)、如图③,是一个城市下水道,下水道入口宽40cm,下水道水平段高度为40cm,现在要想把整根木棒AB通入下水道水平段进行工作,那么这根木棒最长可以是(cm)(直接写出结果,结果四舍五入取整数).
 24. 阅读:对于函数y=ax2+bx+c(a≠0),当t1≤x≤t2时,求y的最值时,主要取决于对称轴x=﹣ 是否在t1≤x≤t2的范围和a的正负:①当对称轴x=﹣ 在t1≤x≤t2之内且a>0时,则x=﹣ 时y有最小值,x=t1或x=t2时y有最大值;②当对称轴x=﹣ 在t1≤x≤t2之内且a<0时,则x=﹣ 时y有最大值,x=t1或x=t2时y有最小值;③当对称轴x=﹣ 不在t1≤x≤t2之内,则函数在x=t1或x=t2时y有最值.
24. 阅读:对于函数y=ax2+bx+c(a≠0),当t1≤x≤t2时,求y的最值时,主要取决于对称轴x=﹣ 是否在t1≤x≤t2的范围和a的正负:①当对称轴x=﹣ 在t1≤x≤t2之内且a>0时,则x=﹣ 时y有最小值,x=t1或x=t2时y有最大值;②当对称轴x=﹣ 在t1≤x≤t2之内且a<0时,则x=﹣ 时y有最大值,x=t1或x=t2时y有最小值;③当对称轴x=﹣ 不在t1≤x≤t2之内,则函数在x=t1或x=t2时y有最值.解决问题:
设二次函数y1=a(x﹣2)2+c(a≠0)的图象与y轴的交点为(0,1),且2a+c=0.
(1)、求a、c的值;(2)、当﹣2≤x≤1时,直接写出函数的最大值和最小值;(3)、对于任意实数k,规定:当﹣2≤x≤1时,关于x的函数y2=y1﹣kx的最小值称为k的“特别值”,记作g(k),求g(k)的解析式;(4)、在(3)的条件下,当“特别值”g(k)=1时,求k的值.