浙江省金华市永康市2016-2017年中考模拟数学考试试卷
试卷更新日期:2017-08-23 类型:中考模拟
一、选择题
-
1. ﹣2017的相反数是( )A、 B、2017 C、﹣2017 D、﹣2.
如图,已知a∥b,∠1=68°,则∠2=( )
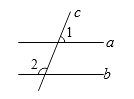 A、22° B、68° C、102° D、112°3. 抛物线y=2x2先向右平移1个单位,再向下平移3个单位得到的抛物线解析式为( )A、y=2(x﹣1)2﹣3 B、y=2(x+1)2﹣3 C、y=2(x﹣1)2+3 D、y=2(x+1)2+34. 下列运算正确的是( )A、a2+a3=a5 B、a2•a3=a6 C、(a2)3=a8 D、a3÷a2=a5.
A、22° B、68° C、102° D、112°3. 抛物线y=2x2先向右平移1个单位,再向下平移3个单位得到的抛物线解析式为( )A、y=2(x﹣1)2﹣3 B、y=2(x+1)2﹣3 C、y=2(x﹣1)2+3 D、y=2(x+1)2+34. 下列运算正确的是( )A、a2+a3=a5 B、a2•a3=a6 C、(a2)3=a8 D、a3÷a2=a5.如图物体的主视图是( )
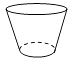 A、
A、 B、
B、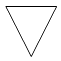 C、
C、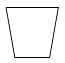 D、
D、 6. 分式方程 的解是( )A、x=1 B、x=﹣1 C、x=2 D、x=﹣27. 如图,在△ABC中,点D,E分别在AB,AC上,且 ,则S△ADE:S△ABC( )
6. 分式方程 的解是( )A、x=1 B、x=﹣1 C、x=2 D、x=﹣27. 如图,在△ABC中,点D,E分别在AB,AC上,且 ,则S△ADE:S△ABC( ) A、1:2 B、1:4 C、1:8 D、1:98. 某校7个班同学积极捐出自己的零花钱献爱心,各班捐款的数额分别是(单位:元):500,200,500,300,500,250,1350.这组数据的众数和中位数分别是( )A、500,200 B、500,500 C、500,300 D、1350,5009. 不等式组 的解在数轴上表示为( )A、
A、1:2 B、1:4 C、1:8 D、1:98. 某校7个班同学积极捐出自己的零花钱献爱心,各班捐款的数额分别是(单位:元):500,200,500,300,500,250,1350.这组数据的众数和中位数分别是( )A、500,200 B、500,500 C、500,300 D、1350,5009. 不等式组 的解在数轴上表示为( )A、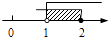 B、
B、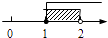 C、
C、 D、
D、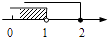 10. 已知A,B两地相距80km,甲,乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车.图中DE,OC分别表示甲,乙离开A地的路程s(km)与时间t(h)的函数关系,根据图象得出的下列信息错误的是( )
10. 已知A,B两地相距80km,甲,乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车.图中DE,OC分别表示甲,乙离开A地的路程s(km)与时间t(h)的函数关系,根据图象得出的下列信息错误的是( )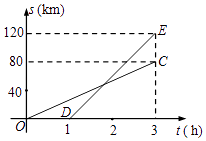 A、乙到达B地时甲距A地120km B、乙出发1.8小时被甲追上 C、甲,乙相距20km时,t为2.4h D、甲的速度是乙的速度的 倍
A、乙到达B地时甲距A地120km B、乙出发1.8小时被甲追上 C、甲,乙相距20km时,t为2.4h D、甲的速度是乙的速度的 倍二、填空题
-
11. 因式分解:x2﹣9= .12. 函数 的自变量x的取值范围是 .13. 如图,⊙O是△ABC的外接圆,∠AOB=70°,AB=AC,则∠ABC= .
 14. 一个布袋里放有红色、黄色、黑色三种球,它们除颜色外其余都相同.红色、黄色、黑色的个数之比为4:3:2,则从布袋里任意摸出1个球不是红球的概率是 .15. 如图,正方形ABCD的边长为13,以CD为斜边向外作Rt△CDE.若点A到CE的距离为17,则CE= .
14. 一个布袋里放有红色、黄色、黑色三种球,它们除颜色外其余都相同.红色、黄色、黑色的个数之比为4:3:2,则从布袋里任意摸出1个球不是红球的概率是 .15. 如图,正方形ABCD的边长为13,以CD为斜边向外作Rt△CDE.若点A到CE的距离为17,则CE= . 16.
16.一张宽为6cm的平行四边形纸带ABCD如图1所示,AB=10cm,小明用这张纸带将底面周长为10cm直三棱柱纸盒的侧面进行包贴(要求包贴时没有重叠部分).小明通过操作后发现此类包贴问题可将直三棱柱的侧面展开进行分析.
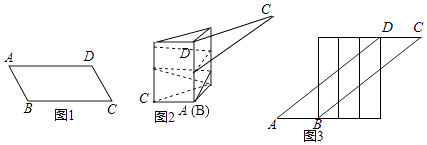 (1)、若纸带在侧面缠绕三圈,正好将这个直三棱柱纸盒的侧面全部包贴满.则纸带AD的长度为 cm;(2)、若AD=100cm,纸带在侧面缠绕多圈,正好将这个直三棱柱纸盒的侧面全部包贴满.则这个直三棱柱纸盒的高度是 cm.
(1)、若纸带在侧面缠绕三圈,正好将这个直三棱柱纸盒的侧面全部包贴满.则纸带AD的长度为 cm;(2)、若AD=100cm,纸带在侧面缠绕多圈,正好将这个直三棱柱纸盒的侧面全部包贴满.则这个直三棱柱纸盒的高度是 cm.三、解答题
-
17. 计算:2cos30°+(﹣2)2+| ﹣2|﹣( )0 .18. 先化简,再求值:(x﹣1)(x+2)﹣(x+1)2 , 其中x=2.19. 如图所示,在▱ABCD中,对角线AC与BD相交于点O,过点O作一条直线分别交AB,CD于点E,F.
 (1)、求证:OE=OF;(2)、若AB=6,BC=5,OE=2,求四边形BCFE的周长.20.
(1)、求证:OE=OF;(2)、若AB=6,BC=5,OE=2,求四边形BCFE的周长.20.小张在甲楼A处向外看,由于受到前面乙楼的遮挡,最近只能看到地面D处,俯角为α.小颖在甲楼B处(B在A的正下方)向外看,最近能看到地面E处,俯角为β,地面上G,F,D,E在同一直线上,已知乙楼高CF为10m,甲乙两楼相距FG为15m,俯角α=45°,β=35°.
 (1)、求点A到地面的距离AG;(2)、求A,B之间的距离.(结果精确到0.1m)
(1)、求点A到地面的距离AG;(2)、求A,B之间的距离.(结果精确到0.1m)(sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
21. 学校计划在七年级学生中开设4个信息技术应用兴趣班,分别为“无人机”班,“3D打印”班,“网页设计”班,“电脑绘画”班,规定每人最多参加一个班,自愿报名.根据报名情况绘制了下面统计图表,
请回答下列问题:
七年级兴趣班报名情况统计表.
兴趣班名称
频率
“无人机”
a
“3D打印”
0.05
“网页设计”
0.25
“电脑绘画”
0.40
(1)、报名参加兴趣班的总人数为人;统计表中的a=;(2)、将统计图补充完整;(3)、为了均衡班级人数,在“电脑绘画”班中至少动员几人到“3D打印”班,才能使“电脑绘画”班人数不超过“3D打印”班人数的2倍?22. 如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上一动点,连结AC并延长交⊙O于D,过点D作圆的切线交OB的延长线于E,已知OA=8. (1)、求证:∠ECD=∠EDC;(2)、若tanA= ,求DE长;(3)、当∠A从15°增大到30°的过程中,求弦AD在圆内扫过的面积.23.
(1)、求证:∠ECD=∠EDC;(2)、若tanA= ,求DE长;(3)、当∠A从15°增大到30°的过程中,求弦AD在圆内扫过的面积.23.探究:如图1,直线l与坐标轴的正半轴分别交于A,B两点,与反比例函数y= (k>0,x>0)的图象交于C,D两点(点C在点D的左边),过点C作CE⊥y轴于点E,过点D作DF⊥x轴于点F,CE与DF交于点G(a,b).
 (1)、若 ,请用含n的代数式表示 ;(2)、
(1)、若 ,请用含n的代数式表示 ;(2)、求证:AC=BD;
应用:如图2,直线l与坐标轴的正半轴分别交于点A,B两点,与反比例函数y= (k>0,x>0)的图象交于点C,D两点(点C在点D的左边),已知 ,△OBD的面积为1,试用含m的代数式表示k.
 24. 已知,抛物线y=ax2+bx+4 与x轴交于点A(﹣3,0)和B(2,0),与y轴交于点C.(1)、求抛物线的解析式;(2)、
24. 已知,抛物线y=ax2+bx+4 与x轴交于点A(﹣3,0)和B(2,0),与y轴交于点C.(1)、求抛物线的解析式;(2)、如图1,若点D为CB的中点,将线段DB绕点D旋转,点B的对应点为点G,当点G恰好落在抛物线的对称轴上时,求点G的坐标;
 (3)、
(3)、如图2,若点D为直线BC或直线AC上的一点,E为x轴上一动点,抛物线

y=ax2+bx+4对称轴上是否存在点F,使以B,D,F,E为顶点的四边形为菱形?若存在,请求出点F的坐标;若不存在,请说明理由.