天津市红桥区2016-2017学年中考三模数学考试试卷
试卷更新日期:2017-08-23 类型:中考模拟
一、选择题
-
1. 计算﹣2+6等于( )A、4 B、8 C、﹣4 D、﹣82. sin60°的值为( )A、 B、 C、 D、3. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、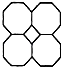 C、
C、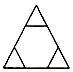 D、
D、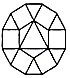 4. 我国倡导的“一带一路”建设将促进我国与世界一些国家的互利合作,根据规划“一带一路”地区覆盖总人口为4400000000人,这个数用科学记数法表示为( )A、44×108 B、4.4×108 C、4.4×109 D、4.4×10105. 如图是由5个相同的小正方体组成的立体图形,这个立体图形的俯视图是( )
4. 我国倡导的“一带一路”建设将促进我国与世界一些国家的互利合作,根据规划“一带一路”地区覆盖总人口为4400000000人,这个数用科学记数法表示为( )A、44×108 B、4.4×108 C、4.4×109 D、4.4×10105. 如图是由5个相同的小正方体组成的立体图形,这个立体图形的俯视图是( )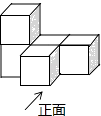 A、
A、 B、
B、 C、
C、 D、
D、 6. 实数n、m是连续整数,如果n<<m,那么m+n的值是( )A、7 B、9 C、11 D、137. 化简 ﹣ 的结果是( )A、a+b B、a C、a﹣b D、b8. 方程x2=2x的解是( )A、x=2 B、x1=2,x2=0 C、x1= ,x2=0 D、x=09. 有理数a在数轴上的位置如图所示,则关于a,﹣a,1的大小关系表示正确的是( )
6. 实数n、m是连续整数,如果n<<m,那么m+n的值是( )A、7 B、9 C、11 D、137. 化简 ﹣ 的结果是( )A、a+b B、a C、a﹣b D、b8. 方程x2=2x的解是( )A、x=2 B、x1=2,x2=0 C、x1= ,x2=0 D、x=09. 有理数a在数轴上的位置如图所示,则关于a,﹣a,1的大小关系表示正确的是( )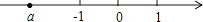 A、a<1<﹣a B、a<﹣a<1 C、1<﹣a<a D、﹣a<a<110. 如图,在矩形ABCD中,AB=1,BC= .将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′的长度为( )
A、a<1<﹣a B、a<﹣a<1 C、1<﹣a<a D、﹣a<a<110. 如图,在矩形ABCD中,AB=1,BC= .将矩形ABCD绕点A逆时针旋转至矩形AB′C′D′,使得点B′恰好落在对角线BD上,连接DD′,则DD′的长度为( )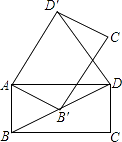 A、 B、 C、 +1 D、211. 如图,Rt△AOC的直角边OC在x轴上,∠ACO=90°,反比例函数y=经过另一条直角边AC的中点D,S△AOC=3,则k=( )
A、 B、 C、 +1 D、211. 如图,Rt△AOC的直角边OC在x轴上,∠ACO=90°,反比例函数y=经过另一条直角边AC的中点D,S△AOC=3,则k=( )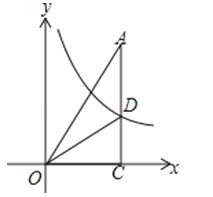 A、2 B、4 C、6 D、312. 如图,点E(x1 , y1),F(x2 , y2)在抛物线y=ax2+bx+c上,且在该抛物线对称轴的同侧(点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C.设S为四边形ABDC的面积.则下列关系正确的是( )
A、2 B、4 C、6 D、312. 如图,点E(x1 , y1),F(x2 , y2)在抛物线y=ax2+bx+c上,且在该抛物线对称轴的同侧(点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C.设S为四边形ABDC的面积.则下列关系正确的是( ) A、S=y2+y1 B、S=y2+2y1 C、S=y2﹣y1 D、S=y2﹣2y1
A、S=y2+y1 B、S=y2+2y1 C、S=y2﹣y1 D、S=y2﹣2y1二、填空题
-
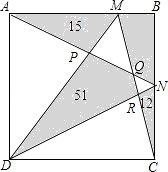
13. 计算4x2y•(﹣ x)= .14. 计算: + = .15. 一个盒子中装有2个白球,5个红球,从这个盒子中随机摸出一个球,是红球的概率为 .16. 已知一次函数y=x+4的图象经过点(m,6),则m= .17. 如图所示,ABCD是一个正方形,其中几块阴影部分的面积如图所示,则四边形BMQN的面积为 .
 18. 如图,在每个小正方形边长为1的网格中,点A,点C均落在格点上,点B为中点.
18. 如图,在每个小正方形边长为1的网格中,点A,点C均落在格点上,点B为中点.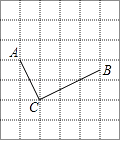
(Ⅰ)计算AB的长等于;
(Ⅱ)若点P,Q分别为线段BC,AC上的动点,且BP=CQ,请在如图所示的网格中,用无刻度的直尺,画出当PQ最短时,点P,Q的位置,并简要说明画图方法(不要求证明) .
三、解答题
-
19. 解不等式组
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得;
(Ⅱ)解不等式②,得;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
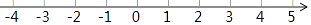
(Ⅳ)原不等式组的解集为 .
20. 某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数(每人投10次)进行整理,作出如下统计图表.进球数(个)
8
7
6
5
4
3
人数
2
1
4
7
8
2

请你根据图表中的信息回答下列问题:
(1)、训练后篮球定时定点投篮人均进球数为个;进球数的中位数为个,众数为个;(2)、该班共有多少学生;(3)、根据测试资料,参加篮球定时定点投篮的学生训练后比训练前的人均进球增加了20%,求参加训练之前的人均进球数(保留一位小数).21. 已知⊙O中,AC为直径,MA、MB分别切⊙O于点A、B.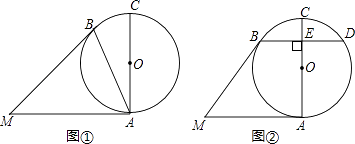 (1)、如图①,若∠BAC=23°,求∠AMB的大小;(2)、如图②,过点B作BD∥MA,交AC于点E,交⊙O于点D,若BD=MA,求∠AMB的大小.22. 如图,一渔船自西向东追赶鱼群,在A处测得某无名小岛C在北偏东60°方向上,前进2海里到达B点,此时测得无名小岛C在东北方向上.已知无名小岛周围2.5海里内有暗礁,问渔船继续追赶鱼群有无触礁危险?(参考数据: )
(1)、如图①,若∠BAC=23°,求∠AMB的大小;(2)、如图②,过点B作BD∥MA,交AC于点E,交⊙O于点D,若BD=MA,求∠AMB的大小.22. 如图,一渔船自西向东追赶鱼群,在A处测得某无名小岛C在北偏东60°方向上,前进2海里到达B点,此时测得无名小岛C在东北方向上.已知无名小岛周围2.5海里内有暗礁,问渔船继续追赶鱼群有无触礁危险?(参考数据: ) 23. 某日王老师佩戴运动手环进行快走锻炼,两次锻炼后数据如表.与第一次锻炼相比,王老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍.设王老师第二次锻炼时平均步长减少的百分率为x(0<x<0.5).
23. 某日王老师佩戴运动手环进行快走锻炼,两次锻炼后数据如表.与第一次锻炼相比,王老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍.设王老师第二次锻炼时平均步长减少的百分率为x(0<x<0.5).项目
第一次锻炼
第二次锻炼
步数(步)
10000
①
平均步长(米/步)
0.6
②
距离(米)
6000
7020
注:步数×平均步长=距离.
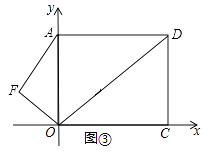
(1)、根据题意完成表格填空;(2)、求x;(3)、王老师发现好友中步数排名第一为24000步,因此在两次锻炼结束后又走了500米,使得总步数恰好为24000步,求王老师这500米的平均步长.24. 已知:如图①,在平面直角坐标系xOy中,A(0,5),C( ,0),AOCD为矩形,AE垂直于对角线OD于E,点F是点E关于y轴的对称点,连AF、OF.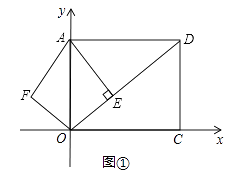 (1)、求AF和OF的长;(2)、如图②,将△OAF绕点O顺时针旋转一个角α(0°<α<180°),记旋转中的△OAF为△OA′F′,在旋转过程中,设A′F′所在的直线与线段AD交于点P,与线段OD交于点Q,是否存在这样的P、Q两点,使△DPQ为等腰三角形?若存在,求出此时点P坐标;若不存在,请说明理由.
(1)、求AF和OF的长;(2)、如图②,将△OAF绕点O顺时针旋转一个角α(0°<α<180°),记旋转中的△OAF为△OA′F′,在旋转过程中,设A′F′所在的直线与线段AD交于点P,与线段OD交于点Q,是否存在这样的P、Q两点,使△DPQ为等腰三角形?若存在,求出此时点P坐标;若不存在,请说明理由.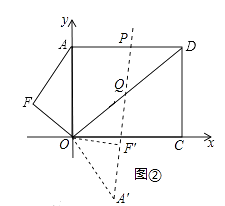
 25. 如图,在平面直角坐标系xOy中,一次函数 (m为常数)的图象与x轴交于点A(﹣3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A,C两点,并与x轴的正半轴交于点B.
25. 如图,在平面直角坐标系xOy中,一次函数 (m为常数)的图象与x轴交于点A(﹣3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A,C两点,并与x轴的正半轴交于点B.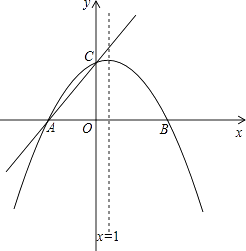 (1)、求m的值及抛物线的函数表达式;(2)、设E是y轴右侧抛物线上一点,过点E作直线AC的平行线交x轴于点F.是否存在这样的点E,使得以A,C,E,F为顶点的四边形是平行四边形?若存在,求出点E的坐标及相应的平行四边形的面积;若不存在,请说明理由;(3)、若P是抛物线对称轴上使△ACP的周长取得最小值的点,过点P任意作一条与y轴不平行的直线交抛物线于M1(x1 , y1),M2(x2 , y2)两点,试探究 是否为定值,并写出探究过程.
(1)、求m的值及抛物线的函数表达式;(2)、设E是y轴右侧抛物线上一点,过点E作直线AC的平行线交x轴于点F.是否存在这样的点E,使得以A,C,E,F为顶点的四边形是平行四边形?若存在,求出点E的坐标及相应的平行四边形的面积;若不存在,请说明理由;(3)、若P是抛物线对称轴上使△ACP的周长取得最小值的点,过点P任意作一条与y轴不平行的直线交抛物线于M1(x1 , y1),M2(x2 , y2)两点,试探究 是否为定值,并写出探究过程.